« Modernizing Kevin Bacon | Main | Fast-modularity made really fast »
February 12, 2007
BK21 - Workshop on Complex Systems
Recently, I've been in Korea attending the BK21 Workshop on Complex Systems [1]. The workshop itself was held on Saturday at the Korean Advanced Institute for Science and Technology (KAIST) [2] where Hawoong Jeong played the part of an extremely hospitable host. The workshop's billing was on complex systems in general, but mainly the six invited speakers emphasized complex networks [3]. Here are some thoughts that popped out during, or as a result of, some of the lectures, along with some less specific thoughts.

Methods of Statistical Mechanics in Complex Network Theory I've enjoyed hearing Juyong Park (Notre Dame University) describe his work on the Exponential Random Graph (ERG) model of networks before, and enjoyed it again today. The ERG model was originally produced by some sociologists and statisticians, but you wouldn't believe it since it fits so well into the statistical mechanics framework. What makes it useful is that, assuming you properly encode your constraints or dynamics into the system, standard statistical mechanics tools let you understand the average features of the resulting set of random graphs. That is, it's a very nice way to define a set of graphs that have particular kinds of structure, but are otherwise random [4].
Even after chatting afterward with Juyong about ERGs in the context of some questions I have on community structure, I'm still not entirely clear how to use this framework to answer complicated questions. It seems that the encoding step I mention above is highly non-trivial, and that even modestly complicated questions, at best, quickly lead first to intractable equations and then to MCMC simulations. At worst, they lead to a wasted day and a broken pencil. Still, if we can develop more powerful tools for the analysis of (realistic) ERG models, I think there's a lot ERGs can offer the field of network theory. I have a personal little goal now to learn enough about ERGs to demonstrate their utility to my students by making them work through some rudimentary calculations with them.
Functional vs Anatomical Connectivity in Complex Brain Networks
Unfortunately, I was somewhat lost during the talk by Changsong Zhou (University of Potsdam) on the dynamics of neuronal networks. Fortunately, while bopping around Seoul's Insadong area a few days later, I had a chance to have him elucidate networks and neuroscience.
Having seen a number of talks on synchronization in complex networks, I've always been puzzled as to why that is the property people seem to care about for dynamic processes on static networks, and not on their information processing or functional behavior. Changsong clarified - if your basic network unit is an oscillator, then synchronization is how information spreads from one location to another. It still seems to me that, at least in neuronal networks, small groups of neurons should behavior more like functional / information processing units rather than like oscillators, but perhaps I'm still missing something here.
The Hierarchical Organization of Network
Oh, and I gave a talk about my work with Mark Newman and Cris Moore on hierarchical random graphs. This was the third (fourth?) time I've given a version of this talk, and I felt pretty good about the set of results I chose to present, and the balance of emphasis I placed on the methodological details and the big picture.
Also, at the last minute before the talk, and because this venue seemed like a good place to make a little plug for statistical rigor, I threw in some slides about the trouble with fitting power laws wily-nily to the tails of distributions [5]. Pleasantly, I saw a lot of nodding heads in the audience during this segment - as if their owners were unconsciously assenting to their understanding. I'd like to think that by showing how power laws and non-power laws can be statistically (and visually!) indistinguishable, most people will be more careful in the language they use in their conclusions and in their modeling assumptions, but I doubt that some will easily give up the comfort that comes with being able to call everything in complex systems a "power law" [6].
Some less specific thoughts
I think a lot of work in the future (or rather, a lot more than has been done in the past) is going to be on biochemical networks. Since biological systems are extremely complicated, this brings up a problem with the way we reduce them to networks, i.e., what we call nodes and what we call edges. For biologists, almost any abstraction we choose is going to be too simple, since it will throw away important aspects like strange neuronal behavior, non-linear dependence, quantum effects, and spatial issues like protein docking. But at the same time, a model that incorporates all of these things will be too complicated to do solve or simulate. My sympathies here actually lay more with the biologists than the networks people (who are mostly physicists), since I'm more interested in understanding how nature actually works than in telling merely plausible stories about the data (which is, in my opinion, what a lot of physicists who work in complex systems do, including those working on networks).
Still, with systems as messy as biological ones, there's a benefit to being able to give an answer at all, even if it's only approximately correct. The hard part in this approach is to accurately estimate the size of the error bars that go with the estimate. That is, rough answers are sufficient (for now) so long as within that roughness lies the true answer. When we use networks built from uncertain data (most networks), and when we use an algorithm-dependent methodology [7] to analyze that data (most analyses), it's not particularly clear how to accurately estimate the corresponding uncertainty in our conclusions. This is a major problem for empirical network science, and I haven't seen many studies handle it well. The moral here is that so long as we don't properly understand how our methods can mislead us, it's not clear what they're actually telling us!
-----
[1] Although I've known about this event for about a month now, I didn't learn until I arrived what the BK21 part meant. BK21 is an educational development program sponsored by the Korean Ministry of Education (jointly with Cornell and Seoul National University) that emphasizes advanced education in seven areas (information technology, biotech, mechanical engineering, chemical engineering, materials science, physics, and chemistry).
[2] KAIST is located in Daejeon, who's main claim to fame is its focus on science and technology - in 1993, Daejeon hosted a three month long international event called Expo '93. On the way into town yesterday, I saw various remnants of the event, including a hill with hedges grown to spell "EXPO '93".
[3] Given the billing, I suppose it's fitting that someone from SFI was there, although its easy to argue these days that "complex systems" is mainstream science, and that complex networks are one of the more visible aspects of the field. What's surprising is that no one from Cornell (the BK21's US partner) was there.
[4] This is very similar to a maximum entropy argument, which physicists adore and machine-learning people are conflicted about.
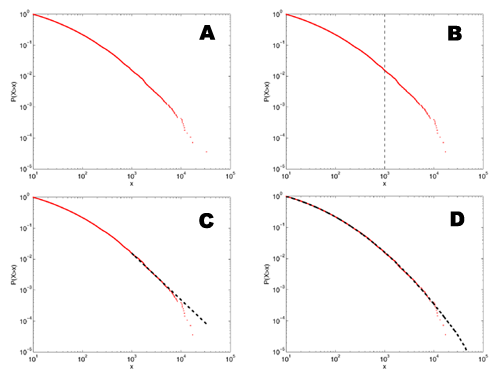
[5]
A: This shows a distribution that we might find in the literature - it has a heavy looking tail that could be a power law, and a slow roll-off in the lower tail.
B: If I eyeball the distribution, at about x=1000, it starts looking particularly straight.
C: If I fit a power-law model to the data above this point, it visually appears to follow the data pretty well. In fact, this kind of fit is much better than many of the ones seen in the physics or biology literature since it's to the cumulative distribution function, rather than the raw density function.
D: The rub, of course, is that this distribution doesn't have a power-law tail at all, but is a log-normal distribution. The only reason it looks like it has a power-law tail is that, for a finite-sized sample, the tail always looks like a power law. The more data we have, the farther out in the tail we have to go to find the "power law" and the steeper the estimated slope will be. If we have some theoretical reason to expect the slope to be less than some value, then this fact may save us from mistaking a lognormal for a power law. The bad news is that it can take a lot more data than we typically have for this to help us.
[6] Power laws have been ridiculously accused of being "the signature of complex systems." Although maybe the person who uttered this statement was being pejorative, in which case, and with much chagrin, I'd have to agree.
[7] What do I mean by "algorithm-dependent methodology"? I basically mean a heuristic approach, i.e., a technique that seems reasonable on the surface, but which ignores whether the solution it produces is correct or optimal. Heuristics often produce "pretty good" solutions, and are often necessary when the optimization version of a problem is hard (e.g., NP-hard). The cost of using a heuristic to find a pretty good solution (in contrast to an approximately correct solution, a la approximation algorithms) is typically that it can also produce quite poor solutions on some problems, and, more importantly here, that they are inherently biased in the range of solutions they do produce. This bias is typically directly a function of the assumptions used to build the heuristic, and, because it can be tricky to analyze, is the reason that uncertainty analysis of heuristics is extremely hard, and thus why computer scientists frown upon their use. Basically, the only reason you should ever use a heuristic is if the more honest methods are too slow for the size of your input. In contrast, an algorithm-independent method is one that is at least unbiased in the way it produces solutions, although it still may not produce an optimum one. MCMC and simulated annealing are examples of unbiased heuristics.
posted February 12, 2007 08:14 AM in Complex Systems | permalink