« Power laws and all that jazz, redux | Main | If you're in Korea this week... »

November 17, 2009

How big is a whale?

One thing I've been working on recently is a project about whale evolution [1]. Yes, whales, those massive and inscrutable aquatic mammals that are apparently the key to saving the world [2]. They've also been called the poster child of macroevolution, which is why I'm interested in them, due to their being so incredibly different from their closest living cousins, who still have four legs and nostrils on the front of their face.

Part of this project requires understanding something about how whale size (mass) and shape (length) are related. This is because in some cases, it's possible to get a notion of how long a whale is (for example, a long dead one buried in Miocene sediments), but it's generally very hard to estimate how heavy it is. [3]

This goes back to an old question in animal morphology, which is whether size and shape are related geometrically or elastically. That is, if I were to double the mass of an animal, would it change its body shape in all directions at once (geometric) or mainly in one direction (elastic)? For some species, like snakes and cloven-hoofed animals (like cows), change is mostly elastic; they mainly get longer (snakes) or wider (bovids, and, some would argue, humans) as they get bigger.

About a decade ago, Marina Silva [4], building on earlier work [5], tackled this question quantitatively for about 30% of all mammal species and, unsurprisingly I think, showed that mammals tend grow geometrically as they change size. In short, yes, mammals are generally spheroids, and L = (const.) x M^(1/3). This model is supposed to be even better for whales: because they're basically neutrally buoyant in water, gravity plays very little role in constraining their shape, and thus there's less reason for them to deviate from the geometric model [6].

Collecting data from primary sources on the length and mass of living whale species, I decided to reproduce Silva's analysis [7]. In this case, I'm using about 2.5 times as much data as Silva had (n=31 species versus n=77 species), so presumably my results are more accurate. Here's a plot of log mass versus log length, which shows a pretty nice allometric scaling relationship between mass (in grams) and length (in meters):

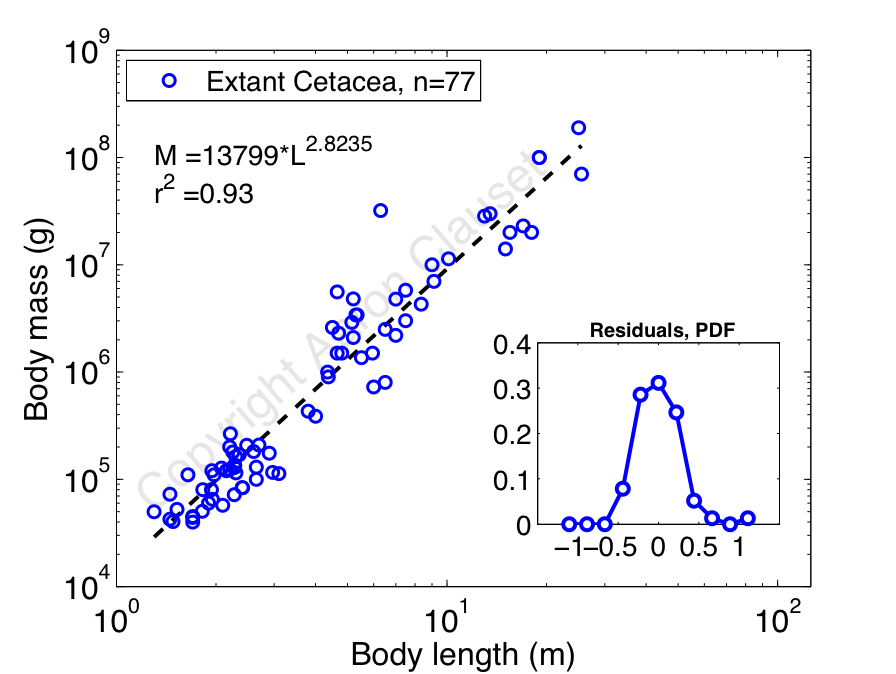
Aside from the fact that mass and length relate very closely, the most interesting thing here is that the estimated scaling exponent is less than 3. If we take the geometric model at face value, then we'd expect the mass of a whole whale to simply be its volume times its density, or

where k_1 and k_2 scale the lengths of the two minor axes (its widths, front-to-back and left-to-right) relative to the major axis (its length L, nose-to-tail), and the trailing constant is the density of whale flesh (here, assumed to be the density of water) [8].

If the constants k_1 and k_2 are the same for all whales (the simplest geometric model), then we'd expect a cubic relation: M = (const.) x L^3. But, our measured exponent is less than 3. So, this implies that k_1 and k_2 cannot be constants, and must instead increase slightly with greater length L. Thus, as a whale gets longer, it gets wider less quickly than we expect from simple geometric scaling. But, that being said, we can't completely rule out the hypothesis that the scatter around the regression line is obscuring a beautifully simple cubic relation, since the 95% confidence intervals around the scaling exponent do actually include 3, but just barely: (2.64, 3.01).

So, the evidence is definitely in the direction of a geometric relationship between a whale's mass and length. That is, to a large extent, a blue whale, which can be 80 feet long (25m), is just a really(!) big bottlenose dolphin, which are usually only 9 feet long (2.9m). That being said, the support for the most simplistic model, i.e., strict geometric scaling with constant k_1 and k_2, is marginal. Instead, something slightly more complicated happens, with a whale's circumference growing more slowly than we'd expect. This kind of behavior could be caused by a mild pressure toward more hydrodynamic forms over the simple geometric forms, since the drag on a longer body should be slightly lower than the drag on a wider body.

Figuring out if that's really the case, though, is beyond me (since I don't know anything about hydrodynamics and drag) and the scope of the project. Instead, it's enough to be able to make a relatively accurate estimation of body mass M from an estimate of body length L. Plus, it's fun to know that big whales are mostly just scaled up versions of little ones.

More about why exactly I need estimates of body mass for will have to wait for another day.

Update 17 Nov. 2009: Changed the 95% CI to 3 significant digits; tip to Cosma.

Update 29 Nov. 2009: Carl Zimmer, one of my favorite science writers, has a nice little post about the way fin whales eat. (Fin whales are almost as large as blue whales, so presumably the mechanics are much the same for blue whales.) It's a fascinating piece, involving the physics of parachutes.

-----

[0] The pictures are, left-to-right, top-to-bottom: blue whale, bottlenose dolphin, humpback whale, sperm whale, beluga, narwhal, Amazon river dolphin, and killer whale.

[1] Actually, I mean Cetaceans, but to keep things simple, I'll refer to whales, dolphins, and porpoises as "whales".

[2] Thankfully, the project doesn't involve networks of whales... If that sounds exciting, try this: D. Lusseau et al. "The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Can geographic isolation explain this unique trait?" Behavioral Ecology and Sociobiology 54(4): 396-405 (2003).

[3] For a terrestrial mammal, it's possible to estimate body size from the shape of its teeth. Basically, mammalian teeth (unlike reptilian teeth) are highly differentiated and certain aspects of their shape correlate strongly with body mass. So, if you happen to find the first molar of a long dead terrestrial mammal, there's a biologist somewhere out there who can tell you both how much it weighed and what it probably ate, even if the tooth is the only thing you have. Much of what we know about mammals from the Jurassic and Triassic, when dinosaurs were dominant, is derived from fossilized teeth rather than full skeletons.

[4] Silva, "Allometric scaling of body length: Elastic or geometric similarity in mammalian design." J. Mammology 79, 20-32 (1998).

[5] Economos, "Elastic and/or geometric similarity in mammalian design?" J. Theoretical Biology 103, 167-172 (1983).

[6] Of course, fully aquatic species may face other biomechanical constraints, due to the drag that water exerts on whales as they move.

[7] Actually, I did the analysis first and then stumbled across her paper, discovering that I'd been scooped more than a decade ago. Still, it's nice to know that this has been looked at before, and that similar conclusions were arrived at.

[8] Blubber has a slight positive buoyancy, and bone has a negative buoyancy, so this value should be pretty close to the true average density of a whale.

posted November 17, 2009 04:33 PM in Evolution | permalink

Comments

Posted by: Cosma Shalizi at November 17, 2009 07:00 PM

Posted by: wayne buckman at December 10, 2009 10:47 AM