« 2010: a year in review | Main | Conference: Applications of Network Theory »

January 08, 2011

Labyrinths, caves and ... power laws?

Late last year, I saw a few references on Facebook to some beautiful pictures of big caves in Vietnam. I didn't realize until later that this wasn't just any big cave, but probably the largest cave in the world Hang Son Doong, which was first surveyed only two years ago. National Geographic did a short article about it and its photo gallery was the source of the beautiful images.

From the article:

In the spring of 2009, [Jonathan] Sims was a member of the first expedition to enter Hang Son Doong, or "mountain river cave," in a remote part of central Vietnam. Hidden in rugged Phong Nha-Ke Bang National Park near the border with Laos, the cave is part of a network of 150 or so caves, many still not surveyed, in the Annamite Mountains. During the first expedition, the team explored two and a half miles of Hang Son Doong before a 200-foot wall of muddy calcite stopped them. They named it the Great Wall of Vietnam. Above it they could make out an open space and traces of light, but they had no idea what lay on the other side. A year later, they have returned —- seven hard-core British cavers, a few scientists, and a crew of porters -— to climb the wall, if they can, measure the passage, and push on, if possible, all the way to the end of the cave.

... An enormous shaft of sunlight plunges into the cave like a waterfall. The hole in the ceiling through which the light cascades is unbelievably large, at least 300 feet across. The light, penetrating deep into the cave, reveals for the first time the mind-blowing proportions of Hang Son Doong. The passage is perhaps 300 feet wide, the ceiling nearly 800 feet tall: room enough for an entire New York City block of 40-story buildings. There are actually wispy clouds up near the ceiling.

The light beaming from above reveals a tower of calcite on the cave floor that is more than 200 feet tall, smothered by ferns, palms, and other jungle plants. Stalactites hang around the edges of the massive skylight like petrified icicles. Vines dangle hundreds of feet from the surface; swifts are diving and cutting in the brilliant column of sunshine. The tableau could have been created by an artist imagining how the world looked millions of years ago.

This cave is truly mind-boggling in size, as the pictures above make clear. Many caves have their own ecosystems, powered either by nutrients flowing in from the surface (sometimes carried by animals like bats that use caves as nesting grounds or garbage dumps) or coming out of the earth itself. It will be interesting to see what weird wonders scientists find in these caves. The third picture shows a forest in the cave where a roof collapse lets light (and life) in.

Coincidentally, only a few weeks before these appeared, I received an email from a gentleman in Norway curious about power-law distributions and caves. As it turns out, an avid American caver named Bob Gulden maintains a global database of cave size information, including data on the longest caves in the world, the deepest caves in the world, and the same for the United States, among other things [1]. The Hang Son Doong cave doesn't show up on Bob's list of the big caves likely because it is not an extremely long or deep cave [2]. Rather, it simply has some of the largest open spaces and towering features. The longest cave in the world is the Mammoth Cave System in Kentucky at 390 miles in length.

The question I was posed by my emailer was basically, does the distribution of large cave lengths that Bob has tabulated follow a power-law distribution? And if so, what does that tell us about the number of shorter caves out there waiting to be discovered? In meters, the top three cave lengths are 627,644, 241,595 and 230,140, while the 300th longest cave is only 15,144 meters long. That huge variance immediately tells us that we're dealing with a heavy-tailed distribution. Being more sophisticated, and doing the statistics properly, here's what the distribution looks like along with a maximum likelihood power-law fit.

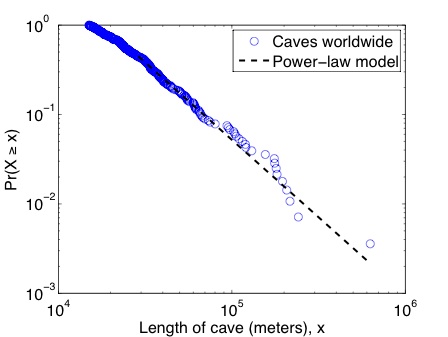
This is not a bad looking fit. The maximum likelihood exponent is alpha = 2.73 +/- 0.19 for the 125 caves 28,968m or longer. Most notably, the p-value for the fitted model is p = 0.38 +/- 0.03, implying that the power-law hypothesis is at least a plausible explanation for the length distribution of the very longest caves in the world [3]. Who would have guessed?

What this means for less long caves is more ambiguous. From a purely statistical point of view, more than half of the 280 caves I analyzed [4] are excluded from the power-law region. This could be a sampling artifact in the sense that shorter caves are probably harder to find than longer ones and thus they are under-represented in our data collection relative to their true frequency. In fact, given that even long caves are quite difficult to find and accurately survey, especially if they are in remote places, have few surface openings, are under water or have many tight squeezes, it seems highly likely that there is also under-reporting and possibly even mis-measurement at the upper end of the distribution, although how much seems difficult to say [5].

If these data are representative of the underlying distribution of worldwide cave lengths, then the non-power-law behavior at the short end could also indicate a mixture of distributional structures, with the power-law-like behavior only applying for the very longest of caves. This then begs the question: what kind of geological or mixture of geological processes produce such a heavy-tailed distribution of cave lengths, and might there be different processes controlling the creation of long versus short caves? Trivial hypotheses based on equating this distribution with fracture length distributions, earthquake sizes, or even the self-similarity of erosion networks might work, but they also might not. For instance, the formation process may depend on the type of rock the cave is in, and rock type does seem to vary among the top 300 longest caves.

For any mechanistic explanation, there's another interesting unknown here, which is how long do caves typically last? For instance, I imagine some kind of geological shuffling process that occasionally creates pockets of air while moving large amounts of rock around. Through additional shuffling, these proto-caves can occasionally become connected and the probability of connecting many pockets together to form a very long cave must depend on the time scale of cave lifetimes. That is, the processes that create the pockets can also eliminate them or divide them. Intuitively, very long caves should be fairly short-lived because they have many more places where a geological shift could disconnect them. Were such events independent, this would yield an effective Poisson process which is clearly not going to produce extremely long caves, although mixtures of these across different time or length scales might do the trick. Other processes may also end up being important, for instance, erosion, which can quickly carve pockets out of certain types of rock, the proximity to a tectonic plate boundary, where geological shuffling is most common, etc. Adding these effects to the simple probabilistic model outlined above could be quite complicated, but would also give us some idea of where to look for new big caves, which would be cool.

-----

[1] Unsurprisingly, there's a whole National Speleological Society devoted to caving, which even publishes a scientific journal called the Journal of Cave and Karst Studies. An earlier version of Bob's list, listing only the top 53 caves, appeared in JCKS in 2006.

[2] For the "world's longest" list, Bob tracks only caves with length greater than 15000 meters, or about 9.3 miles in length. But see footnote [4].

[3] Said more precisely, the p-value is sufficiently large that we cannot reject the hypothesis that the fluctuations (deviations) observed between the fitted model and the data are simply iid sampling noise.

[4] Bob updates his list pretty regularly, so these numbers are from the list as of today, while the data I pulled and analyzed was from 18 December 2010.

[5] There are other lists of long caves, for instance, one formerly maintained by Eric Madelaine in France (here). Eric's list seems to have been dormant since 2006 but has a total of 1628 entries including caves as short as 3000 meters. Additionally, some measurements differ from Bob's list. Here, the maximum likelihood power-law region is much larger, extending down to xmin = 3,950m and including 1214 caves, the tail heavier, with alpha = 2.27 +/- 0.06, but the power-law hypothesis is highly unlikely, with p = 0.05 +/- 0.03. What this means, of course, is still fairly unclear, as many of the same sampling and measurement issues described above apply here just as forcefully. What I think these analyses do tell us is that cave length is a fairly non-trivial variable, and that there are likely interesting geological processes shaping its clear heavy-tailed structure. Whether it's a nice power law or not is really beside the point, and real progress would take the form of a mechanistic hypothesis that can be tested.

Update 8 January 2011: As an afterthought, given that the larger data set with the wider "power-law region" in [5] yields a much heavier value of alpha relative to Bob's smaller data set (alpha = 2.27 vs. 2.73), and the former is largely a superset of the latter, it seems to me that the power-law-like structure is probably a sampling artifact. Thus, a much larger data set (n>10,000) seems likely to show significant curvature throughout most of the range of cave lengths (which would explain why the exponent increased from the smaller xmin to the larger one) or perhaps simply statistically significant deviations relative to the simple power-law model. The extreme upper tail (Bob's data) would still hint at power-law structure, but this might merely indicate some geologically induced finite-size limit.

posted January 8, 2011 11:54 AM in Scientifically Speaking | permalink

Comments

Posted by: Edenjoy @ Seasonal Affective Disorder Light Therapy at January 11, 2011 08:04 PM

Posted by: John at January 19, 2011 07:36 AM

Posted by: automated forex trading at January 19, 2011 07:52 PM

Posted by: Cristopher Moore at January 30, 2011 02:07 PM

Posted by: Digital Photo Basics at February 6, 2011 10:34 PM

Posted by: Eugena Ezzelle at February 6, 2011 10:51 PM