5: The Pseudosphere

On the large-scale, much of our universe is three-dimensional, hyperbolic space curved into the fourth dimension. In order to understand what three-dimensional hyperbolic space is like, we will look into two-dimensional Hyperbolic Space. Two-dimensional, spherical geometry (the geometry of spherical space) is best represented as the surface of a sphere. Two-dimensional, hyperbolic geometry is best represented as the surface of a pseudosphere. But what is a pseudosphere?

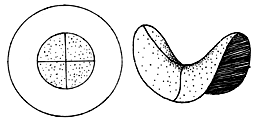
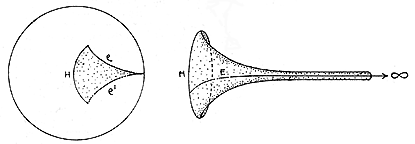
A pseudosphere, like a sphere, can be thought of as a 2-D surface. The sphere is smaller than the plane: it bends back on itself and is finite, whereas the plane is infinite. A pseudosphere, however, is bigger than the plane. Both plane and pseudosphere are infinite, yet the pseudosphere manages to have more room. You might say that the pseudosphere is more intensely infinite then the plane.

Precisely because the pseudosphere is actually bigger than the plane, it is very hard to represent it in the normal Euclidean geometry of our drawings. But there is a special trick for shrinking a pseudosphere to fit inside a circular boundary. This trick is called, "The Poincaré Model of hyperbolic geometry", and it is precisely the model used in NonEuclid. Figures A, B and C below are screen captures of NonEuclid. In each figure, the encompassing, white circle is the Boundary Circle of the shrunken pseudosphere. Shrinking the pseudosphere to fit into a bounded disk distorts the pseudosphere, but it distorts it in a very careful way. The disk of the Poincaré Model is geometrically equivalent to the original pseudosphere! In-other-words, any Theorem that we prove in the Poincaré Model, we are guaranteed will be a Theorem in the original Pseudosphere.

Figure 5a: Congruent Line Segments that Share an Endpoint.
Figure 5b: Segments 0.25, 0.5, 1.0, 2.0, 4.0, 8.0 and 16.0 Units in Length.
Figure 5c: Tessellation of Congruent Triangles.

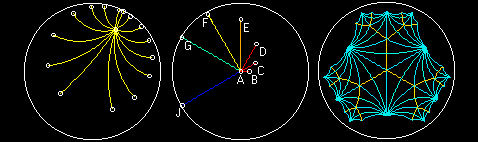
As a point becomes closer to the Boundary Circle, its distance from the center approaches infinity. Figure-5a shows a set of Straight, Hyperbolic, Line Segments all of Length 3.00 units. Noticed that the closer a segment is to the Boundary Circle, the "shorter" it appears. This set of segments can be thought of as radii of a circle (since they are congruent, and have a common endpoint).

The set of segments in Figure-5b, have a common endpoint at the center of the Boundary Circle. Segment AB has a length of 0.25 units. Segment AC has a length of 0.5 units. Going clockwise, each segment is twice as long as the previous segment. The last two segments (AG and AJ) appear to be the same length, yet AJ, (half a pixel longer), has twice the length of AG!.

Depending on the resolution of your monitor, when you are using NonEuclid to plot points, you will notice that the cursor never gets more then about ten distance units from the center before it pops out of the model. This is because on a computer screen we are limited to a pixel granularity. However, the distance between that last computer dot within the boundary, and the actual boundary is infinite.

Although it is impossible to smoothly stretch out the whole pseudosphere in our space, we can stretch out pieces of it to get various, bounded surfaces. By thinking about what happens if we stretch pieces of the pseudosphere out to proper size, we begin to get an idea of the full surface. Figure 5d and 5f are by David Povilaitis, and are excerpts from Rudy Rucker's "The Fourth Dimension".

Figure 5d - A Disk cut from the Pseudosphere Stretches into a Saddle Shape. [Rucker-84]

Figure 5e - Disk Shaped Sectors of Equal Radius, but cut from Different Locations of thePseudosphere each Stretch out to form Identical Saddles.

Figure 5f - A Sector of the Pseudosphere, cut to the "Infinitely Distant Boundary", Stretches intoa Horn. [Rucker-84]

NonEuclid Home