Constructing The Dragon

Figure 1: Level 13 of The Dragon

Figure 1: Level 13 of The Dragon
There is an infinite verity of widely different fractal patterns that can be generated by repeated folding and unfolding of a strip of colored paper. The fractal shown above is the particular Paper Folding Fractal pattern that would result if you were able to fold a strip of paper exactly in half thirteen times, and carefully open it up so that each fold makes a perfect 90° angle. This particular pattern is commonly called "The Dragon" and was popularized in the film "Jurassic Park".
The Paper-Folding-Fractals software was used to create The Dragon shown above. This software can be used to create many other paper folding fractals.
The Dragon: Step-by-Step:
A good way to learn about this fractal is
to get about 5 strips of paper (10 or 11 inches long) and actually construct
the first few levels.
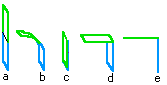
Figure 2: Construction of Level
1 of The Dragon
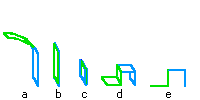
Level 3 of The Dragon is produced by folding the paper in-half 3 times to the left, and opening it up to eight sides and seven right angles (figure 4a). Figure 4b is Level 3 as seen from directly above. Level 4 is produced by folding 4 times to the left. Notice the box shape that forms in level 4 - notice that the paper DOES NOT cross to form this box. In level 13 (shown in figure 1), there are thousands of these boxes. After level 4, it begins to get a bit difficult to build the Dragon with paper. If you are practiced with paper folding, then you might have come across the cardinal rule of Origami: "Though shalt not fold any normal size piece of paper more then seven times in the same place".
However, who says we are limited to a normal size piece of paper? I worked with a 6th grade class that was able to produce level 9 of the Dragon from 14 inch strips of construction paper. Each student was able to work separately on a 14 inch strip to produce a part of the Dragon. We then assembled the pieces on a bulletin board. Each student had been given a different color construction paper; therefore, the level 9 Dragon had a color scheme similar to that used in figure 1 above.
But lets backup a bit. Before we can have students doing this parallel processing work, we need to find a pattern in the Dragon that allows us to build in it separate pieces without actually folding a single, gigantic strip of paper in-half 9 times.
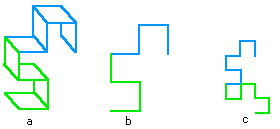
Look back at figure 3. Notice that the first half of level 4 is an exact copy of level 3 (except each side in level 4 is half the length of each side in level 3). The second half of level 4 is also an exact copy of level 3. Likewise, to build level 5 you could create two separate copies of level 4, rotated one 90° with respect to the other, and tape the two together end-to-end. How many copies of level 4 would you need to build level 6? How many students were needed to create the bulletin board filling, level 9 Dragon from 14 inch strips of colored construction paper?