Lecture 04 Computer Data Representation Part 3
Joseph Haugh
University of New Mexico
Bits, Bytes, and Integers
- Integers
- Representation: unsigned and signed (CS241L)
- Conversion, casting
- Expanding and truncating
- Addition, negation, multiplication, shifting
- Summary
- Representations in memory, pointers, strings
Unsigned and Signed Numeric Values
| X | B2U(X) | B2T(X) |
|---|---|---|
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | -8 |
| 1001 | 9 | -7 |
| 1010 | 10 | -6 |
| 1011 | 11 | -5 |
| 1100 | 12 | -4 |
| 1101 | 13 | -3 |
| 1110 | 14 | -2 |
| 1111 | 15 | -1 |
- Equivalence
- Same encodings for nonnegative values
- Uniqueness
- Every bit pattern represents unique integer value and vice versa
- Can Invert Mappings
- U2B(x) = B2U−1(x)
- Bit pattern for unsigned integer
- T2B(x) = B2T−1(x)
- Bit pattern for two’s comp integer
- U2B(x) = B2U−1(x)
Mapping Between Signed and Unsigned
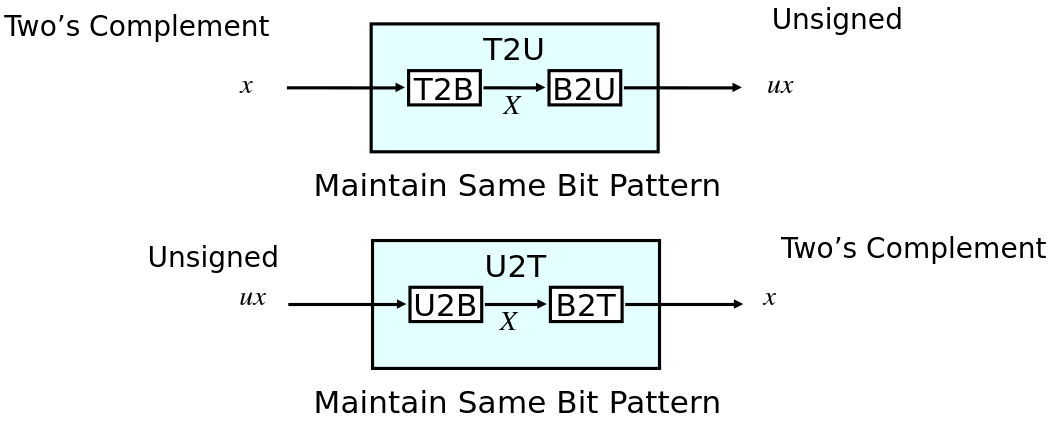
- Mappings between unsigned and two’s complement numbers:
- Keep bit representations and reinterpret
Mapping Signed to Unsigned
| Bits | Signed | Unsigned |
|---|---|---|
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | -8 | 8 |
| 1001 | -7 | 9 |
| 1010 | -6 | 10 |
| 1011 | -5 | 11 |
| 1100 | -4 | 12 |
| 1101 | -3 | 13 |
| 1110 | -2 | 14 |
| 1111 | -1 | 15 |
Relation Between Signed and Unsigned
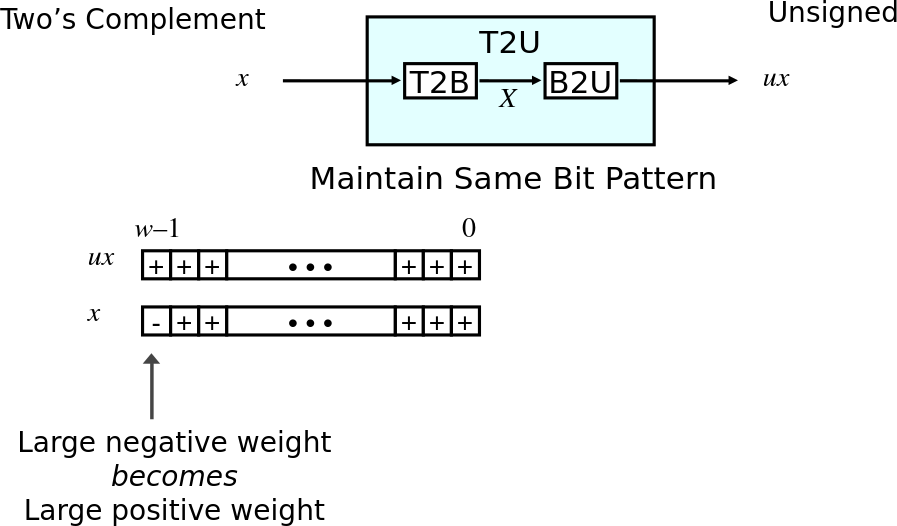
Conversion Visualized
- Twos complement -> Unsigned
- Ordering inversion
- Negative -> Big positive
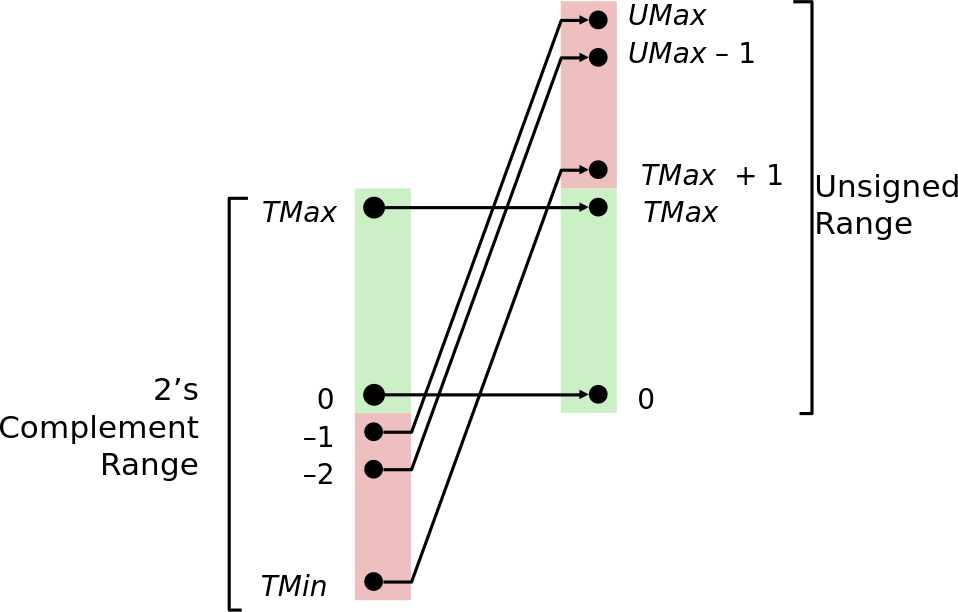
Signed vs Unsigned in C
- Constants
- By default are considered to be signed integers
- Unsigned if have “U” as suffix
0U,4294967259U
Signed vs Unsigned in C
Casting
Explicit casting between signed & unsigned same as
U2TandT2Uint tx, ty; unsigned ux, uy; tx = (int) ux; uy = (unsigned) ty;
Implicit casting also occurs via assignments and procedure calls
tx = ux; uy = ty;
Casting Surprises
- Expression Evaluation
- If there is a mix of unsigned and signed in single expression, signed values implicitly cast to unsigned
- Including comparison operations
<, >, ==, <=, >= - Examples for
W = 32:TMIN = -2,147,483,648TMAX = 2,147,483,647
- Note: signed means two’s complement
Casting Surprises Cont.
| Constant1 | Relation | Constant2 | Type | Eval |
|---|---|---|---|---|
| 0 | == | 0U | unsigned | 1 |
| -1 | < | 0 | signed | 1 |
| -1 | < | 0U | unsigned | 0* |
| 2147483647 | > | -2147483647-1 | signed | 1 |
| 2147483647U | > | -2147483647-1 | unsigned | 0* |
| -1 | > | -2 | signed | 1 |
| (unsigned)-1 | > | -2 | unsigned | 1 |
| 2147483647 | > | (int) 2147483648U | signed | 1* |
- On your own, justify each *
Summary: Casting Signed <–> Unsigned
- Bit pattern is maintained but reinterpreted
- Can have unexpected effects: adding or subtracting 2w (24 in examples with 4 bits)
- Expression containing signed and unsigned int: int is cast to unsigned!!
Bits, Bytes, and Integers
- Integers
- Representation: unsigned and signed (CS241L)
- Conversion, casting
- Expanding and truncating
- Addition, negation, multiplication, shifting
- Summary
- Representations in memory, pointers, strings
Expanding and Truncating: Sign Extension
- Task:
- Given w-bit signed integer x
- Convert it to w+k-bit integer with same value
- Rule:
- Make k copies of sign bit: X′ = xw–1, …, xw–1, xw–1, xw–2, …, x0
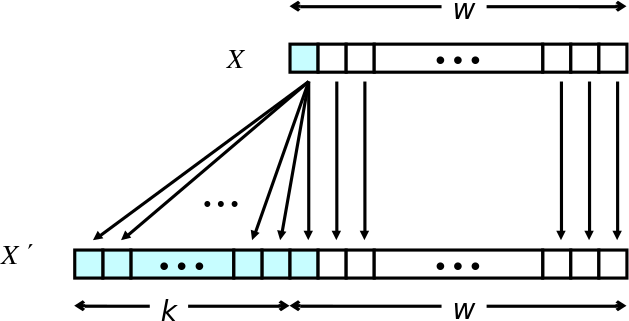
Sign Extension Example
short int x = 15213;
int ix = (int) x;
short int y = -15213;
int iy = (int) y;| Decimal | Hex | Binary | |
|---|---|---|---|
| x | 15213 | 3B 6D | 00111011 01101101 |
| ix | 15213 | 00 00 3B 6D | 00000000 00000000 00111011 01101101 |
| y | -15213 | C4 93 | 11000100 10010011 |
| iy | -15213 | FF FF C4 93 | 11111111 11111111 11000100 10010011 |
- Converting from smaller to larger integer data type
- C automatically performs sign extension
Practice Problem 2.22
- Show that each of the following bit vectors is, a two’s-complement representation of -5 by applying Equation 2.3 (conv. B2T)
- 1011
- 11011
- 111011
Truncation: Unsigned
- Say you have an unsigned variable,
x - Truncating
xtokbits is the same as x mod 2k - For example:
- x = 248 = 11111000
- Truncating to
4bits: x = 1000 = 8 - 248 mod 24 = 8
Truncation: Signed
- Say you have a signed variable,
x - Truncating
xtokbits is the same as U2Tk(x mod 2k) - For example:
- x = 248 = 11111000
- Truncating to
4bits: x = 1000 = −8 - U2T4(248 mod 24) = −8
Practice Problem: 2.24
- Truncate from
4to3bits
| Hex | Unsigned Original | Unsigned Truncated | Two’s Complement Original | Two’s Complement Truncated |
|---|---|---|---|---|
| 0 | 0 | 0 | ||
| 2 | 2 | 2 | ||
| 9 | 9 | -7 | ||
| B | 11 | -5 | ||
| F | 15 | -1 |
Practice Problem: 2.24
| Hex | Unsigned Original | Unsigned Truncated | Two’s Complement Original | Two’s Complement Truncated |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 2 | 2 | 2 |
| 9 | 9 | 1 | -7 | 1 |
| B | 11 | 3 | -5 | 3 |
| F | 15 | 7 | -1 | -1 |
Summary: Expanding and Truncating
- Expanding (e.g., short int to int)
- Unsigned: zeros added
- Signed: sign extension
- Both yield expected result
- Truncating (e.g., unsigned to unsigned short)
- Unsigned/signed: bits are truncated
- Result reinterpreted
- Unsigned: mod operation
- Signed: similar to mod
- For small numbers yields expected behavior
Bits, Bytes, and Integers
- Integers
- Representation: unsigned and signed (CS241L)
- Conversion, casting
- Expanding and truncating
- Addition, negation, multiplication, shifting
- Summary
- Representations in memory, pointers, strings
Arithmetic: Basic Rules
- Most PL support “fixed-size arithmetic” (~= integers)
- Addition:
- Unsigned/signed: Normal addition followed by truncate,
- same operation on bit level
- Unsigned: addition mod 2w
- Mathematical addition + possible subtraction of 2w (on overflow)
- Signed: modified addition mod 2w (result in proper range)
- Mathematical addition + possible addition or subtraction of 2w
Arithmetic: Basic Rules
- Multiplication:
- Unsigned/signed: Normal multiplication followed by truncate, same operation on bit level
- Unsigned: multiplication mod 2w
- Signed: modified multiplication mod 2w (result in proper range)
Unsigned Addition
- Operands: w bits
- True sum: w + 1 bits
- Discard carry: w bits

- Standard Addition Function
- Ignores carry output
- Implements Modular Arithmetic
- s = UAddw(u, v) = u + v mod 2w
- Detecting overflow occurred: check if s < u or s < v
Unsigned Addition: Example
- Wraps Around
- If true sum ≥ 2w
- At most once
- For example: with w = 4, lets add 9 + 21:
| Binary | Decimal | Mod 4 | |
|---|---|---|---|
| 1001 | 9 | 9 | |
| + | 1100 | 12 | 12 |
| 1 | 0101 | 21 | 5 |
Two’s Complement Addition
- Operands: w bits
- True sum: w + 1 bits
- Discard carry: w bits

TAddandUAddhave Identical Bit-Level Behavior- Signed vs. unsigned addition in C:
- int s, t, u, v;
- s = (int) ((unsigned) u + (unsigned) v);
- t = u + v
- Will give s = = t
TAdd Overflow
- Functionality
- True sum requires w+1 bits
- Drop off MSB
- Treat remaining bits as 2’s comp. integer
- Detect overflow
- 2 pos, sum neg
- 2 neg, sum pos
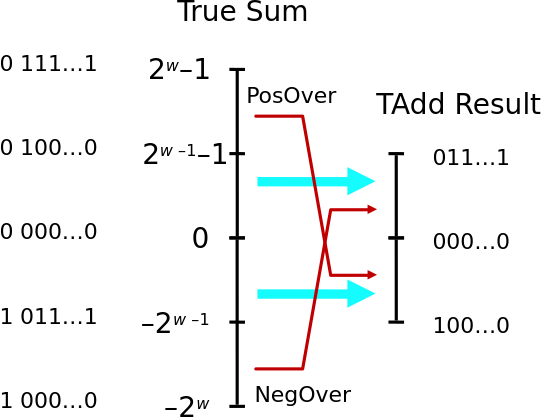
Overflow Examples
- Negative Overflow, w = 4
| Binary | Decimal | Mod 4 | |
|---|---|---|---|
| 1101 | -3 | -3 | |
| + | 1000 | -8 | -8 |
| 1 | 0101 | -11 | 5 |
- Positive Overflow, w = 4
| Binary | Decimal | |
|---|---|---|
| 0011 | 3 | |
| + | 0111 | 7 |
| 1010 | -6 |
Study and Practice on your Own
- In all arithmetic operations, for unsigned and signed, there are principles used to compute the operations and their derivation. Follow and study the derivations on your own. (Derivations start p. 72 (2.5) to p. 106
- Problem 2.29, p. 93 (understand 2’s comp +)
- Problem 2.33, p. 95
Example: Problem 2.29, First Row
| Binary | Decimal | Mod 5 | |
|---|---|---|---|
| 10100 | -12 | -12 | |
| + | 10001 | -15 | -15 |
| 1 | 00101 | -27 | 5 |
Unsigned Multiplication
- Operands: w bits
- True product: 2 * w bits
- Discard carry: w bits

- Standard Multiplication Function
- Ignores high order w bits
- Implements Modular Arithmetic
- UMultw(u, v) = u * v mod 2w
Two’s Complement Multiplication
- Operands: w bits
- True product: 2 * w bits
- Discard carry: w bits

- Standard Multiplication Function
- Ignores high order w bits
- Lower bits are the same
- TMultw(u, v) = U2Tw(u * v mod 2w)
More Practice
- Problem 2.34, p. 98
- Problem 2.35, p. 99