Assiomi e Teoremi

1 Assiomi della geometria di Euclide

Accanto al grande valore pratico rappresentato dallo studio della Geometria i Greci trovavano in essa un grande appagamento estetico. Come i bambini assemblano le costruzioni per costruire fantastiche torri i matematici, a partire da poche definizioni e da un numero ridotto di assunzioni, sono capaci di dimostrare molti teoremi. Mentre i blocchi vengono assemblati con le mani gli assiomi vengono formulati razionalmente.

Tutta la geometria euclidea, che consiste in migliaia di teoremi, deriva da un numero abbastanza esiguo di assunzioni di partenza note come assiomi di Euclide. Nella formulazione di Playfair (1795) i postulati di Euclide sono che:

A-1 si possa tracciare una retta da un punto qualsiasi a un punto qualsiasi;

A-2 si possa prolungare indefinitamente una linea retta;

A-3 si possa costruire una circonferenza di centro e raggio qualsiasi (ciò implica che le distanze non hanno limite. In altri termini, fissato un valore della distanza, è sempre possibile determinare una distanza maggiore o minore);

A-4 tutti gli angoli retti sono tra loro congruenti;

A-5 (Assioma di Parallelismo): data una retta r ed un punto P esterno ad essa esiste un'unica retta s passante per P e parallela ad r.

La geometria euclidea è fondata oltre che sugli assiomi precedenti su un numero di nozioni comuni o regole logiche che Euclide elenca negli "Elementi":

CN-1 cose uguali ad una medesima cosa sono uguali tra loro;

CN-2 sommando a cose uguali una stessa cosa si ottengono ancora cose uguali;

CN-3 sottraendo a cose uguali una stessa cosa si ottengono ancora cose uguali;

CN-4 cose che coincidono l'una con l'altra sono uguali tra loro;

CN-5 l'intero è maggiore della parte.

All'interno del la geometria euclidea assiomi e nozioni comuni hanno come proprietà fondamentali: (1) di essere in numero esiguo, (2) di essere talmente evidenti da risultare inoppugnabili. Per più di duemila anni i matematici non riuscirono a comprendere che il quinto assioma, l'assioma di parallelismo, non era essenziale per la costruzione della geometria e che potevano esistere geometrie in cui esso veniva sostituito da un diverso assioma. Molti tra essi tentarono infruttuosamente di dimostrare che il quinto assioma discendeva dai rimanenti. Solo nei primi anni del XIX secolo due matematici posero fine a tutti i tentativi di dimostrazione. Ivanovitch Lobachevski in Russia e János Bolyai in Ungheria riuscirono infatti a sviluppare una geometria (la geometria iperbolica) in cui si negava l'assioma di parallelismo. Anche i padri della geometria iperbolica non erano in grado di sapere se nello sviluppo della loro teoria si dovesse ad un certo punto giungere ad una contraddizione logica. In questo modo si sarebbe dimostrato che l'assioma di parallelismo era inconsistente con i precedenti quattro assiomi. Tuttavia la contraddizione non fu mai trovata. Al contrario, con lo sviluppo della geometria differenziale, introdotta dal matematico Bernard Riemann, altre ad aprirsi l'orizzonte su un nuovo tipo di geometria (la geometria ellittica), si rese possibile la scoperta di numerosi modelli euclidei della geometria iperbolica. Di questi modelli i più famosi sono quelli di Poincaré, Beltrami e Klein. Attraverso questi modelli fu possibile dimostrare che la geometria iperbolica ha lo stesso grado di consistenza della geometria euclidea e che l'assioma di parallelismo è indipendente dai precedenti assiomi. Questa scoperta ha avuto profonde conseguenze in filosofia in quanto ha intaccato l'idea che la geometria rappresentasse una scienza completamente a priori, la cui validità trascendeva ogni possibile esperienza. Ora noi sappiamo invece che alcuni teoremi valgono solo in alcune geometrie mentre sono falsi in altre.

La negazione dell'assioma di parallelismo può avvenire in due modi:

Assioma di Parallelismo in Geometria Ellittica: data una retta r e un punto P ad essa non appartenente non esistono rette passanti per P e parallele a r.
Assioma di Parallelismo in Geometria Iperbolica: data una retta r e un punto P ad essa non appartenente esistono almeno due rette passanti per P e parallele a r.

Facciamo osservare che quando si parla di parallelismo non si intende che due rette sono parallele se si comportano come i "binari della ferrovia". "Parallele" significa solo che le rette, giacenti su uno stesso piano, non si intersecano in alcun punto.

L'assioma di parallelismo, in geometria ellittica, è inconsistente con i primi quattro assiomi della geometria di Euclide. Se ci riferiamo, come esempio, alla geometria sulla sfera, in cui le rette sono i cerchi massimi, osserviamo che nella maggior parte dei casi, scelti due punti A e B, essi giacciono su uno e un solo cerchio massimo; tuttavia nel caso in cui A e B siano antipodali allora esistono una infinità di cerchi massimi passanti per essi. Ciò contraddice il primo assioma di Euclide. Non è difficile vedere che anche il secondo assioma di Euclide è contraddetto in quanto, se sulla sfera si prolunga un segmento (sferico) al più si ottengono punti coincidenti.

Contrariamente alle aspettative, forse anche di Lobachevski e Bolyai, l'assioma di parallelismo in geometria iperbolica è perfettamente consistente con tutti i rimanenti assiomi euclidei. In altri termini la geometria euclidea e la geometria iperbolica differiscono negli assiomi solo per l'assioma di parallelismo.

2 Altri Assiomi

Oltre agli assiomi e alle nozioni comuni incluse da Euclide nel suo trattato di fatto, nello sviluppo della geometria euclidea, si fa uso di un certo numero di assunzioni implicite. Il merito di aver chiarito questo punto spetta ad Hilbert che ha formulato gli assiomi della geometria in modo rigoroso dando ad essi un'organizzazione ineccepibile. Nell'assiomatica di Hilbert, accanto ai precedenti, compaiono gli assiomi di ordinamento come ad esempio: "dati tre punti su una retta solo uno tra essi giace tra i rimanenti due". Altri assiomi riguardano la congruenza come ad esempio che: "se due triangoli hanno due lati congruenti e l'angolo tra essi compreso uguale allora essi sono congruenti".

3 Dimostrazioni in geometria iperbolica

Come abbiamo visto in precedenza, da un punto di vista degli assiomi, l'unica differenza tra geometria euclidea e iperbolica è rappresentata dall'assioma di parallelismo.

Questa osservazione ha importantissime ripercussioni in relazione alle dimostrazioni di teoremi. Infatti ogni volta che una dimostrazione di geometria euclidea viene condotta senza ricorrere all'assioma di parallelismo essa risulta automaticamente valida anche in geometria iperbolica!

Analogamente, un qualsiasi enunciato di geometria euclidea la cui dimostrazione implichi l'uso dell'assioma di parallelismo risulta automaticamente falso in geometria iperbolica. Un esempio notevole è rappresentato dal teorema che afferma che la somma degli angoli interni di un qualsiasi triangolo è pari a 180°. In Figura 5.4a viene richiamata l'idea della dimostrazione del teorema e da essa si comprende la ragione per cui il teorema deve essere falso in geometria iperbolica.

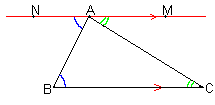
Figura 5.4a

In geometria euclidea, dato un qualsiasi triangolo ABC, esiste unica la retta parallela a BC passante per A. Oltre a questo, se ricordiamo il teorema che afferma che due rette parallele intersecate da una trasversale formano angoli alterno interni di uguale ampiezza, abbiamo direttamente la tesi. La dimostrazione risulta ovviamente impraticabile in geometria iperbolica dove, per un punto esterno ad una retta, passano almeno due rette parallele alla retta data.

Pagina Iniziale
Successivo - Area