CS 432 Project 4: Subband Coding *
In this project, you will experiment with a method for image
compression called subband coding. Subband coding involves
three stages: 1) analysis; 2) quantization; and 3) synthesis. In the
analysis stage, the image is decomposed into a set of sampled bandpass
images. Because the bandpass images typically have a smaller range of
grey values than the original image, reconstructions of comparable
image quality can be achieved using fewer grey levels. Furthermore,
because many grey values in the bandpass image are quite small, the
process of quantization creates long runs of zeros which can be
efficiently compressed using lossless methods. The final stage in
subband coding is termed synthesis, and involves inverting the
analysis stage by reconstructing the unfiltered image from its
bandpass components. The various schemes for subband coding differ in
the particular methods employed in each of the three stages. In this
project, you will use a Laplacian pyramid transform for
analysis and its inverse for synthesis.
Laplacian Pyramids
Laplacian pyramids were introduced in the early 1980's by Peter Burt**
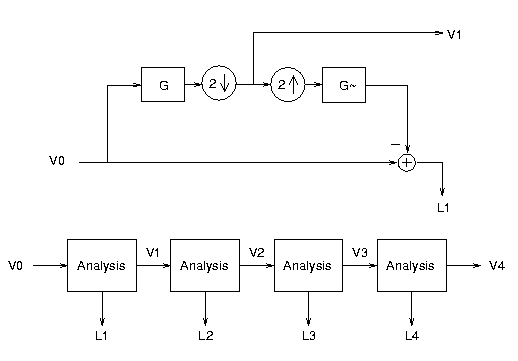
and Ted Adelson. The basic idea is quite simple. First, convolve the
input image, V0, with a Gaussian lowpass filter and then downsample it
to create an image with half the number of rows and columns, V1 (this
is called the reduce operation). Second,
upsample and interpolate the values of V1 to create an image with the
same number of rows and columns as V0 (this is called the project operation). Third, subtract this image
from V0. The resulting image, L1, represents the difference (or error)
between the original image and the downsampled lowpass filtered image.
L1 is equivalent to V0 convolved with a difference of Gaussians
bandpass filter.*** This analysis process can be repeated to
produce V2 and L2 from V1 (and so on). The lowpass filtered and
undersampled images (i.e., V0, V1, V2, V3 and V4) form the levels of a
Gaussian (or lowpass) pyramid. The images representing the differences
between adjacent levels (i.e., L1, L2, L3, and L4) form the levels of
a Laplacian (or bandpass) pyramid.
V0  V1
V1  V2
V2  V3
V3  V4
V4 
L1  L2
L2  L3
L3  L4
L4 
The original image, V0, can be reconstructed (without error) solely
from the Laplacian pyramid levels (i.e., L1, L2, L3, and L4) and the
final level of the Gaussian pyramid (i.e., V4). First, the values of
V4 are upsampled and interpolated to form an image with the same
number of rows and columns as L4. This image is added to L4 to
reconstruct V3. This synthesis process is then repeated until
V0 is reconstructed.
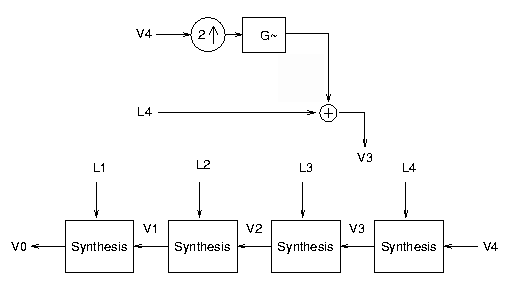
Image Compression
By itself, the Laplacian pyramid is not an image compression scheme.
Indeed, the amount of space required to store the Laplacian pyramid is
33% greater than the amount of space required to store the original
image. However, because of the smaller range of grey values in the
bandpass images, we can use fewer grey levels and yet achieve
reconstructions of comparable image quality. In addition, because many
of the grey values are very small, quantization produces many zero
values. This results in further space savings if a standard
lossless compression scheme is used after quantization.
Project Outline
You will begin by writing two kroutines called Reduce and
Project.
- Reduce---Inputs an image of unspecified size and of type
DOUBLE and outputs a Gaussian convolved image with half the number of
rows and columns and of type DOUBLE.
- Project---Inputs an image of unspecified size and type
DOUBLE and outputs a Gaussian interpolated image with twice the number
of rows and columns and of type DOUBLE.
These kroutines will in turn be used as components in two encapsulated
workspaces called Laplacian Pyramid and Invert Laplacian
Pyramid.
- Laplacian Pyramid---Inputs an image of unspecified size and
type UNSIGNED BYTE and outputs 1) four bandpass images representing
the levels of a four-level Laplacian pyramid; and 2) one lowpass image
representing the fifth level of a Gaussian pyramid. The output images
should be of type DOUBLE.
- Invert Laplacian Pyramid---Inputs 1) four bandpass images
representing the levels of a four-level Laplacian pyramid; and 2) one
lowpass image representing the fifth level of a Gaussian pyramid.
Outputs an image of type UNSIGNED BYTE representing the reconstructed
image.
After you have finished and tested your implementation of the
Laplacian pyramid transform, you will estimate the compression ratios
which can be achieved by using different levels of transform
coefficient quantization. To do this, you will need to implement three
encapsulated workspaces, Sigmoid, Quantize, and
Sigmoid^-1.
- Sigmoid---Inputs an image, x, of unspecified size
and type DOUBLE and outputs an image, y =
256 / (1 + exp(-x/10)), of type UNSIGNED BYTE.
- Quantize---Inputs an image, x, of type UNSIGNED BYTE
and an integer, k, and outputs an image, y = floor(x/2^k)*2^k, of type
UNSIGNED BYTE.
- Sigmoid^-1---Inputs an image, x, of type UNSIGNED
BYTE and outputs an image, y = -10 ln
(256/x - 1) , of type DOUBLE.
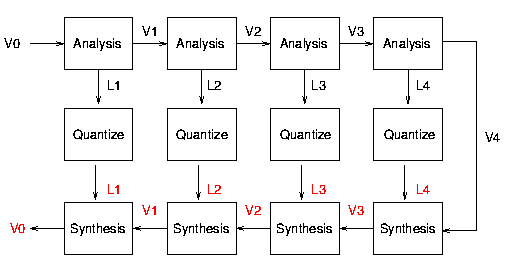
Your Cantata workspace will look something like the workspace
shown below:
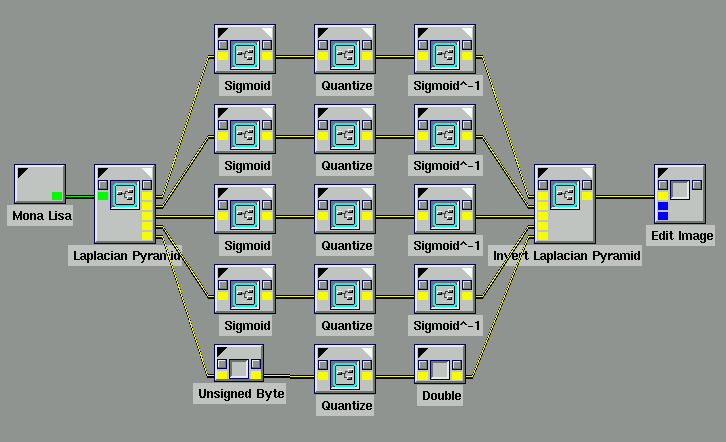
Note that Sigmoid is not applied to the final Gaussian pyramid
level (i.e., V4), only to the four Laplacian pyramid levels (i.e., L1,
L2, L3, and L4). The UNSIGNED BYTE outputs of the five Quantize
glyphs can be stored to disk in .pnm format. We define the
compression ratio to be the ratio of the amount of space
required to store the .pnm file representing the original image
and the amount of space required to store the five .pnm files
representing the Laplacian pyramid and the final Gaussian pyramid
level (where all files are compressed with the UNIX compress utility).
Hints
- You may assume that the row and column size of the input
image are integral powers of two.
- You can use the Khoros library function kpds_set_attribute to change
the size of the output data object. For example,
kpds_set_attribute(out_obj, KPDS_VALUE_SIZE, w/2, h/2, d, 1, 1)
reduces the height and width of the output data object by a factor of two each.
- The Khoros library function, kmalloc, works just like the
standard C library function, malloc. You can use it to create a
buffer to hold intermediate results.
What You Should Hand In
You should hand in a concise (less than 10 page) research report
describing your project. The following should be included either in
the body of the report (where appropriate) or in an appendix:
- Listings of the C source code for the Reduce and Project
kroutines.
- Screen dumps showing the component glyphs and links of the
encapsulated workspaces, Laplacian Pyramid, Invert Laplacian
Pyramid, Sigmoid, Quantize, and Sigmoid^-1.
- Hardcopy of a Gaussian lowpass pyramid computed for the image
of your choice.
- Hardcopy of a Laplacian bandpass pyramid computed for the same
image.
- Hardcopy of the image reconstructed from the Laplacian pyramid without
quantization or compression.
- Histograms of V4, L4, L3, L2 and L1.
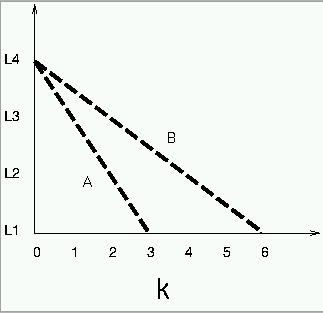
- Calculate the compression ratio for your image using bit
allocation scheme, A.
- Hardcopy of the image reconstructed
from the Laplacian pyramid using bit allocation scheme, A.
- Calculate the compression ratio for your image using bit
allocation scheme, B.
- Hardcopy of the image reconstructed from the Laplacian
pyramid using bit allocation scheme, B.
When You Should Hand It In
The above should be handed in at the beginning of class, Mon. May 1.
Of Possible Interest
* This webpage is located at http://cs.unm.edu/~williams/cs432/project4s00.html
** A fellow U. Mass. Amherst alumnus!
*** The difference of Gaussians is a very good approximation to the
Laplacian of Gaussian.


 V1
V1  V2
V2  V3
V3  V4
V4 
 L2
L2  L3
L3  L4
L4 



