Programming Lang & Systems
Table of Contents
- meta
- class notes
- 2010-01-19 Tue
- 2010-01-21 Thu
- 2010-01-26 Tue
- 2010-01-28 Thu
- 2010-02-02 Tue
- 2010-02-04 Thu
- 2010-02-09 Tue
- 2010-02-11 Thu
- 2010-02-16 Tue
- 2010-02-18 Thu
- 2010-02-23 Tue
- 2010-02-25 Thu
- 2010-03-02 Tue
- 2010-03-04 Thu
- 2010-03-09 Tue
- 2010-03-23 Tue
- 2010-03-30 Tue
- 2010-04-01 Thu
- 2010-04-06 Tue
- 2010-04-08 Thu
- 2010-04-13 Tue
- 2010-04-15 Thu
- 2010-04-20 Tue
- 2010-04-22 Thu
- 2010-04-27 Tue
- 2010-04-29 Thu
- 2010-05-04 Tue
- 2010-05-06 Thu
- Topics
- lisp paper – λ the ultimate imperative
- group theory
- calculating least fixed points
- classic PL papers
- quantifier-elimination … automatically generating inductive assertions
- proving termination with multiset orderings
- "fifth generation computing"
- cardinality of sets – sizes of infinity
- axiomatic semantics
- related books
- Project – Non Von Neumann programming paradigms [5/5]
- Terms
- Theorems and Lemmas
meta
- Collaboration Policy
- only collaborate with Depak, better shot at the comps if we do the homework on our own
- office hours
-
Wednesdays: 2 to 3PM Fridays: 2:30 to 4PM.
class notes
2010-01-19 Tue
Deepak Kapur – focus Automated Theorem Proving
no sufficient text book, material will come from lectures
define syntax & semantics
- formalist
- (platonic ideals are not real) everything is syntax -- there is nothing more than symbol manipulation
- syntax
- symbols, grammar: rules specifying valid program text
- semantics
- meaning
syntax
Backus Naur Form (BNF) define languages through production rules
context free
- non-terminal -> finite string of terminal and non-terminal symbols
- e.g. A -> a B a
regular languages
- non-terminal -> single terminal followed by a single non-terminal
Turing language or "type 0" language
- any collection of terminals and non-terminals -> any collection of terminals and non-terminals
A language consists of…
- alphabet \(\Sigma = \{a, b, c\}\)
- all finite strings taken from \(\Sigma\), \(\Sigma^{*}\)
- palindromes
for example, the language of palindromes $$ P \subset \Sigma^* = {w | w^R=w} $$ can be generated using the following rules- B -> λ – empty string
- B -> a
- B -> b
- B -> c
- B -> d
- B -> e
- B -> aBa
- B -> bBb
- B -> cBc
- B -> dBd
- B -> eBe
we use induction over the size of the strings to prove that these rules only generate palindromes
- hypothesis – assume ∀ w s.t. |w|<k and B->w w==wR
- inductive step…
semantics
we'll be informally using typed set theory to describe the semantics of programming languages
Denotational semantics (providing a rigorous understanding of recursion in the 60s and or 70s) used concepts from topology in particular a theorem due to Tarski dealing with fixed points.
syntactically valid statements w/no semantic value
this statement is false
Cantor was writing the authoritative book on set theory.
- is there a universal set?
-
Russel brought up a problem set
set of all sets that don't contain themselves
this led to types, membership relation can't relate things of the same type can be used to avoid sets that contain themselves
If you have types and strong recursion implies that you must have some small portion of your language which is not well typed
John McArthy wrote lisp which was one of the first languages which could be used to implement its own interpreter.
2010-01-21 Thu
high-level programming paradigms
- functional: manipulating functions, no state (e.g. lambda calculus by Alonzo Church and Haskell Curry)
- logical: manipulating formulas/relations, no state (e.g. Prolog by Kowalski, Colemaurer, Hewitt)
- imperative: manipulating state, (e.g. machine language, asm, Fortran, Cobol, Algol, C, etc…)
if we have some free time read some books on the history of programming languages
quick lambda calculus review
Syntax
-
expressions
- variable / identifier
- abstraction: if e is an expression and v is a variable then (λ (v) e) is an expression
- application: if e1 and e2 are expressions then (e1 e2) is an expression, the application of e1 to e2
Computation: sequence of application of the following rules
-
β-rule: evaluates an application of an abstraction to an expression
- ((λ (x) e) e2) -> replace all free occurrences of x in e with e2
- α-rule: expressions are equal up to universal uniform variable renaming, and the α-rule allows you to rename bound formal parameters
- η-rule: (λ (x) (e x)) -> e
There are a number of possibilities when calculating
-
with some expressions you can keep applying the β-rule
infinitely, for example the following
((\lambda (x) (x x)) (\lambda (x) (x x)))
- when you can't apply the β-rule any more you have a normal form
-
some expressions terminate along some paths and don't terminate
along other paths, for example the following
((\lambda (x) (\lambda (y) y)) ((\lambda (x) (x x)) (\lambda (x) (x x))))
Church-Rosser Theorem: any expression e has a single unique (modulo the α-rule) normal form, however it is possible that some paths of computation from e terminate and some don't terminate
Turing Church Thesis: e is computable by a Turing-machine iff e is computable by λ-calculus
combinatory logic: like λ-calculus with no λ and no variables
variable capture: y could be captured in the following expression
((\lambda (z) (\lambda (y) z)) (\lambda (x) y))
which can be change via the α rule to
((\lambda (z1) (\lambda (y1) z1)) (\lambda (x1) y))
we are advised to always rename variables in this way to create unique variables whenever we have the opportunity
2010-01-26 Tue
Y-operator – recursion
((\lambda (f) ((\lambda (x) (f (x x))) (\lambda (x) (f (x x))))) g)
will end up nesting
((\lambda (x) (f (x x))) (\lambda (x) (f (x x))))
inside of an infinite nesting of applications of g – recursion.
this is the Y-operator
Boolean values
- true – (λ (x) (λ (y) x))
- false – (λ (x) (λ (y) y))
so (T e1 e2) = e1, and (F e1 e2) = e2
so not is
(\lambda (x) (x F T))
natural numbers
need a 0 and a +1 operator
-
0
(\lambda (f) (\lambda (x) x))
-
1
(\lambda (f) (\lambda (x) (f x)))
-
2
(\lambda (f) (\lambda (x) (f (f x))))
so what's the successor function?
(\lambda (n) (\lambda (f) (\lambda (x) (f (f n x)))))
sum
(\lambda (n) (\lambda (m) (\lambda (f) (n f m))))
with the examples of 2 and 3 we get (2 f 3), or
(\lambda (f) (\lambda (x) (f (f (f x))))) (f (\lambda (x) (f (f x))))
now moving from λ calculus to logic
is about ∧, ∨, ¬ , ⇒, ⇔, ⊕
as well as ∀, ∃, =
in logic programming everything is relations
so the predicate view of not is as a relation on two arguments which holds iff they have different truth values
not(x,y)
| T | F |
| F | T |
plus(j, k, l)
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 2 | 2 |
| 2 | 0 | 2 |
| 1 | 1 | 2 |
relations always have one more argument than the related function
2010-01-28 Thu
logic programming
first a recursive factorial
(defn fact [x] (if (= 1 x) 1 (* (fact (dec x)) x)))
now factorial in logic programming
- base case !P (1, 1).
- further cases !P (s(x),y) :- !P (x,z), *P (s(x), y, z)
now with append
- append-P(nil, y, y).
- append-P([a|x], y, [a|z]) :- append-P(x, y, z)
in both of these cases the :- is something like reverse implication, generally we call the left of ":-" the "head" and the rest the body, so
HEAD :- BODY
implementation of these functions… should the following hold
!P(s(s(s(0))), s(s(s(0))))
in logic programming the computation goes form the top down…
- the first rule doesn't apply because s(s(s(0))) != 1
-
then we pattern match against the second rule, so x=s(s(0)) and
y=s(s(s(0))), so the body says
!P(2,z), *P(3, z, 3)
we then recurse again and we get x=1, z=? :!P(1,z), *P(2, z1, z) we now know that z must be 1, and we go back up with z equal to 1 in our previous *P and we get
*P(2, 1, Y)
so Y must equal 2, but it already equals 3
lets look at the "stack"
- !P(s(2),3) :- !P(2,z) *P(s(2), z, 3)
- !P(s(1),z) :- !P(1,z1) *P(s(1), z1, z)
- !P(1,z1) :- (1,1)
- so moving back up with z1 = 1
- *P(s(1), 1, z)
- so z == 1 and going up again we get
- *P(s(2), 1, 3) which is a contradiction
append(I1, I2, [1, 2])
-
first answer
- I1 = nil
- I2 = [1, 2]
-
it will then go back and try to find out which other rules are applicable
- I1 = [A1 | X1]
- I2 = Y1
- [A1 | Z1] = [1, 2]
- A1 = 1
- Z1 = 2
- append(X1, Y1, Z1)
- … basically it gives you all three possible combinations
terminology and conventions
- query: a function call, a set of initial states and you want to see if and what satisfies them, a predicate symbol with a set of terms
- relations are named by predicate symbols
-
terms: argument to predicate symbols
- variable
- constant
- functor applied to a term
- functors are the basic functions in the language (e.g. cons)
- atom: is a predicate symbol applied on terms
- ground term: a term w/o variables
- clause: disjunction of a finite set of literals (or'd together)
- literal: is an atom or its negation
- Horn clauses: most logic programming only deals with Horn clauses, these are clauses in which at most one literal is positive – most of the time we will have exactly one positive literal
- logic program: the conjunction of a finite set of Horn clauses
2010-02-02 Tue
logic programming
review – what is logic program
A logic program is finite set of Horn clauses, and the goal is to find either yes or no and in the case of yes find substitutions for variables which make it true.
A collection of goals (atoms)
$$? G_1(\ldots), G_2(\ldots), \ldots G_p(\ldots)$$So, what's the control flow like?
- goals are processed left to right
-
given a goal to be achieved, it is compared to the program (set of
Horn clauses)from top to bottom. processing means looking for a
clause in the program that unifies with the goal
- if the clause has a head and a body then if the goal unifies with the head it is replaced by the body
- if a clause with a head and no body matches the goal then the goal is simply removed from the list and we remember which clause satisfied the goal
- if there is no clause that unifies with the goal, then the query fails or you do backtracking and try other clauses
backtracking means going back to previous goal, and seeing if there is a different way to satisfy that goal
- if so
- then moving forward with that new satisfaction
- if not
- then moving to the previous goal, if no more previously satisfied goals, then it fails
lets exercise this with an example
program
- \(!P(1,1)\)
- \(!P(s(x),y) :- !P(x,z), *P(s(x),z,y)\)
goal
- \(!P(U,6)\)
evaluation
- compare \(!P(U,6)\) to \(!P(1,1)\) and it fails
- compare \(!P(U,6)\) to \(!P(s(x),y) :- !P(x,z), *P(s(x),z,y)\) and it works so replace it with the body
- we now have \(!P(x_1,z_1)\) and \(*P(s(x_1),z_1,y_1)\) where \(Y_1 = 6\)
- we compare \(!P(x_1,z_1)\) to \(!P(1,1)\) and its satisfied with \(x_1 = z_1 = 1\), so we move on to the next goal
- we compare \(*P(s(1),1,6)\) to multiplication and it fails so we backtrack
- we compare \(!P(x_1,z_1)\) to \(!P(s(x),y) :- !P(x,z), *P(s(x),z,y)\) and we get \(!P(x_2,z_2)\), and \(*P(s(x_2), z_2 y_2)\)
- note: at this point we have three goals, the two mentioned above, and \(!P(x_1,z_1)\) with \(x_1 = s(x_2)\) and \(z_1 = y_2\), and \(U=s(x_1)\)
- we now compare \(!P(x_2, z_2)\) to \(!P(1,1)\) and we get \(x_2 = 1\) and \(z_2 = 1\) which moving forward gives us \(*P(s(x_2), z_2, y_2)\) and \(*P(s(x_1), z_1, y_1)\) with is \(*P(3, 2, 6)\)
this is a search tree, we will be drawing these in homework 2, these are sometimes called and-or trees.
two views of this program
- the intersection of all relations that satisfy the axioms of a program is the meaning of the program, and is also the fixed point of the program.
- or the more computational view, where this relation is the result of computationally building up all the instances satisfying this relation
interpretations of a logic program
The semantics (or meaning) of a logic program is the set of relations corresponding to all predicate symbols in the program.
this set of relations can be constructed bottom up, or by taking the intersection of all of the set of relations which are satisfied by that which satisfies the given program
primitives
relations which are already defined in the language.
in constraint logic programming the primitives permit returning multiple satisfying instances, e.g. \(*P(?,?,6)\) could return all pairs of numbers which multiply to 6.
crash course in unification
2010-02-04 Thu
Herbrand stuff
Jacques Herbrand – one of the first people to define computational inference systems for first-order logic
we'll talk about
- Herbrand Universe
- all possible ground terms which can be constructed using symbols (or functor-symbols) in the program -- the objects between which relations are being defined. This will be finite if there are no function symbols and infinite if there are any function symbols
- Herbrand Base
- every possible application of our relational systems against the elements of our Herbrand Universe -- regardless of whether the relation holds or is true over those elements
- Herbrand Interpretation
- is any subset of the Herbrand Base
- Herbrand Model
-
subset of the Herbrand Base in which every
clause is valid
- a small note on clause validity. A clause \(H :- L_1, L_k\) is valid iff all ground substitutions on \(L_1\) through \(L_k\) are in the interpretation, and ground substitutions on $H$ are also in the model.
- Operational Semantics
- the minimal Herbrand Model, or the intersection of all Herbrand Models for a program
The Herbrand Base is trivially a Herbrand Model of every possible logic program.
in the following factorial definition
- !P(1, 1)
- !P(s(x), y) :- !P(x, z), *P(s(x), z, y)
- *P(0, x, 0)
- *P(s(x), y, z) :- *P(x, y, z1), +P(y, z1, z)
- +P(0, x, x)
- +P(s(x), y, s(z)) :- +P(x, y, z)
the
- Herbrand Universe is 1, s(1), s(s(1)), … and 0, s(0), s(s(0)), …
- Herbrand Base all of the ways that elements of the Herbrand Universe can be packed into the predicates of our program, e.g. !P(1,1), !P(1, s(s(0))), …
- Herbrand Model enough relations validating all clauses, e.g. !P(1,1), !P(2,2), *P(2,1,2), …, !P(3, 6), …
in the homework…
- if M1 and M2 are Herbrand Models, then M1 ∩ M2 are also a Herbrand Model – proof by contradiction
The meaning of a logic program is the intersection of all of its Herbrand Models.
Two logic programs are equivalent if their minimal Herbrand Models are subsets of each other.
a function on Herbrand Interpretations
TP is an operator associated with a program P which converts one Herbrand Interpretation (HI) and transforms it into another HI. It closes the input HI with respect to the clauses – in other words it adds the head of any clause who's body is fully present in HI.
TP(HI) = {σ(H) | H :- L1 … Lk, ∀ i ∈ [1 … k] σ(Li) ∈ HI}
note this is only one step of computation.
- TP0(HI) = ∅
- TP1(∅) = \{σ(H) | H ∈ P\}
- TPi+1(∅) = TPi (TP(∅))
the union of all \(T_P^i\) will equal the meaning of the program
since HI1 ⊆ HI2 → TP(HI1) ⊆ TP(HI2), TP is a monotonic function
One last good definition which we'll need later on. with the subset ordering on sets the least upper bound on a set of sets is their union. a function $f$ is continuous if f(∪i Xi) = ∪i f(Xi). It turns out the Tp is continuous.
One more last definition. Given a function f: D → D. We say x is a fixed point of f iff f(x) = x.
2010-02-09 Tue
questions and review
When evaluating a query with multiple parts (conjunctions) you read the first part of the query and evaluate until you find a first solution, and once it is found you add the next conjunction and continue.
From the first homework one common problem was application of the α-rule to free variables – when it should only be applied to bound variables.
λ-calculus semantics
the semantics of λ-calculus is determined by equivalence classes determined through either
- equivalence classes over transformation via α-rule and β-rule (with β-rule moving in both directions)
- Church-Russle where e1 and e2 are equivalent iff \(\exists e\) s.t. \(e_1 \rightarrow^* e\) and \(e_2 \rightarrow^* e\) – basically picking a normal representative of the equivalence class
no state
logic programming semantics
The semantics of a logic program is the minimal model or the intersection of all models of the program.
no state
simple imperative language
constructs
-
control
- assignments
- if-then-else
- sequences
- louf (while)
-
data types
- Booleans
- numbers
- unbound
This has a notion of state and memory, where a program is a function from state to state.
our discussion/reference of/to states will be
- implicit
- where we talk about properties of states (e.g. "x is even"), state(α) will be all the states in which α is true
- explicit
simple imperative program
x = M y = N z = 0 while y > 0 do if y.even? then x = 2*x y = y/2 else x = 2*x y = y/2 z = z+x end end puts z
| M | N | z |
|---|---|---|
| 1 | 1 | 2… |
| 1 | 2 | 4… |
| 1 | 3 | 6… |
| 2 | 1 | 4… |
| 2 | 2 | 8… |
| 2 | 3 | 12… |
| 3 | 1 | 6… |
| 3 | 2 | 12… |
| 3 | 3 | 18… |
| 3 | 4 | 24… |
| 5 | 3 | 30… |
| 3 | 6 | 36… |
| 7 | 4 | 56… |
so a property of this program is that upon termination \(z = 2*M*N\) and \(x = M * N^{ceil(log_2{N})}\) at the beginning of the program any state can hold so the property is just the formula \(true\)
after a single round of execution the following formulas hold
- \(x = M\)
- \(y = N\)
after another round of execution the following formulas hold
- \(\forall i (0 \leq i \leq ceil(log_2{n})) \wedge x = M * 2 \wedge y = \frac{N}{2^i} \wedge (\ldots)\)
termination
- find some property of the state which continue to decrease and can not do so indefinitely
2010-02-11 Thu
returning to our simple program
1 x := M
2 y := N
3 z := 0
4 while y > 0 do
5 if even(y) then
6 {x := 2x; y := y/2}
9.1
7 {x := 2x; y := y/2; z := z+x;}
9.2
10 end
8
some properties of the program
- \(x_{i+1} = 2x_i\)
- \(y_{i+1} = \frac{y_i}{2}\)
-
\(z_{i+1}\) is tough because we would need an
if
if we have a formula \(\phi(x,y,z)\) which specifies a property of our
state at 4, then we can ensure that the following is true at 9.1
\(\phi(\frac{x}{2},2y,z)\), and similarly at =9.2= we know that
\(\phi(\frac{x}{2},2y+1,z-x)\)
in addition we can say some more things at these places,
-
at
9.1we can say \(even(y_{previous})\) -
at
9.2we can say \(odd(y_{previous})\)
we can think of our imperative programs as operating on formulas specifying properties of our state.
current state at a location $l$ specified by the property \(\phi(l)\). We have a statement $S$ and we can specify the semantics of $S$ as the effect of $S$ on the strongest property. So if \(\phi\) is our strongest property then the difference between \(\phi(l_i)\) and \(\phi(l_{i=1})\) is the _meaning_ of S. we have forward and backward transitions
- forward sometimes we know where we are (our state/property) and we want to find all of the possible places we can go to from here
- backward we know where we are (our state/property) and we want to know all the possible places we could have come from
Basically its all just applying the correct transforms to the arguments to a property statement so that it stays true as the arguments are manipulated by your imperative program.
when moving forward and performing a substitution like the following
x := x + z
we can do the following \(\{\exists t_1 s.t. x = \{x + z\}|_x^{t_1} \vee \phi\}\) if we have \(\phi = \{x + y + 2z = 4\}\) and we perform
x := x + z
then we can say \(\{\exists t_1, x = (x+z)|_x^{t_1} \wedge x + y + 2z = 4\}\) or \(\exists t_1 (x = t_1+z) \wedge t_1 + y + z = 4\) Floyd-Hoare semantics, Axiomatic Semantics: \((\{pre\}, S, \{post\})\), these are called Hoare Triples.
weak and strong states
- α is a property and states(α) is the set of states in which α is true
- states(true) is everything
- states(false) is \(\emptyset\)
- α → β means states(α) ⊆ states(β)
a stronger statement is satisfied by a smaller set of states
2010-02-16 Tue
Two ways to axiomatize the semantics of assignment, weakest precondition and strongest postcondition.
x := e
- forward: \(t_1 := x\), \(x := e|^{t_1}_x\), \(\{\Phi\} \, x := x\{\exists t_1 (x = e|^{t_1}_x \wedge \Phi|_{t_1}^x)\}\)
- backwards: \(\{\alpha|^e_x\}\), \(x := e\{\alpha\}\), \(wp(x := e, \alpha)\)
noop – meaning nothing is done
- wp(noop, α) = α
- wp(s1:s2, α) = wp(s1, wp(s2, α))
so for an if example
-
\(wp(if \, b \, then \, s1 \, else \, s2, \alpha) = \beta\), so
- \((\beta \wedge b \Rightarrow wp(s1, \alpha))\) and
- \((\beta \wedge \not b \Rightarrow wp(s2, \alpha))\)
and for a while example
-
\(wp(while \, b \, do \, S, \alpha) = \beta\)
- \((\beta \wedge b \Rightarrow wp(S, wp(while \, b \, do \, S, \alpha)))\)
- \((\beta \wedge \not b \Rightarrow wp(noop, \alpha))\) which is equal to \((\beta \wedge \not b \Rightarrow \alpha)\)
now, going back to our favorite program…
x = M y = N z = 0 while y > 0 do if y.even? then x = 2*x y = y/2 else x = 2*x y = y/2 z = z+x end end puts z\(\beta \Leftrightarrow (xy + z = 2MN) = \alpha\)
- if \(\not b\), so if \(y \equiv 0\) then \((xy + z = 2MN)\) and \(\alpha\) and we win
-
if $b$, then we do \(\alpha|^{\frac{y}{2}}_y|^{2x}_x\{x := 2x, y =
\frac{y}{2}\} \Leftrightarrow 2x*\frac{y}{2}+z = zMN\)
- \((\beta \wedge even(y)) \Rightarrow 2x\frac{y}{2}+z = zMN\)
-
\((\beta \wedge odd(y)) \Rightarrow 2xy+z = zMN\)
gets a little shaky below here…
\((\beta \wedge odd(y)) \Rightarrow (((\beta|^{z+x}_z)|^{\frac{y}{2}}_y)|^{2x}_x)\)
- \(\Leftrightarrow ((z + x + xy = 2MN)|^{\frac{y}{2}}_y)|^{2x}_x\)
- \(\Leftrightarrow z + zx + 2x \frac{y}{2} = 2MN\)
- \(\Leftrightarrow zxy + z + xy = 2MN\)
2010-02-18 Thu
on the homework when we give semantics we should specify them using wp (Weakest Preconditions) statements
to continue with our famous program…
- assertion/invariant map – is a mapping from locations in the program to formulas/assertions
a loop invariant is an assertion mapped to the beginning of a loop
a verification condition is a pure formula which contains no code
- static analysis
- tries to prove some easy properties about programs through analysis of the program w/o execution
- dynamic analysis
- analysis of a program which involves examining the program during execution
- total correctness
- given an input spec then both the program terminates and the output spec is satisfied
- partial correctness
- given an input spec and assuming the program terminates then the output spec is satisfied
two statements are equivalent if ∀ α, wp(S1,α) = wp(S2,α)
2010-02-23 Tue
a = 0 s = 1 t = 1 while s <= N do a = a + 1 s = s + t + 2 t = t + 2 end puts "a=#{a}, s=#{s}, t=#{t}"
| n | values at termination |
|---|---|
| 1 | a=1, s=4, t=3 |
| 2 | a=1, s=4, t=3 |
| 3 | a=1, s=4, t=3 |
| 4 | a=2, s=9, t=5 |
| 5 | a=2, s=9, t=5 |
| 6 | a=2, s=9, t=5 |
| 7 | a=2, s=9, t=5 |
| 8 | a=2, s=9, t=5 |
| 9 | a=3, s=16, t=7 |
| 10 | a=3, s=16, t=7 |
| 11 | a=3, s=16, t=7 |
| 12 | a=3, s=16, t=7 |
| 13 | a=3, s=16, t=7 |
| 14 | a=3, s=16, t=7 |
| 15 | a=3, s=16, t=7 |
| 16 | a=4, s=25, t=9 |
| 17 | a=4, s=25, t=9 |
| 18 | a=4, s=25, t=9 |
invariants
- t = 2a+1
- s = (a+1)2 – this is not an inductive invariant, as simple backwards semantics turns s=(a+1)2 into s+t+2=(a+2)2, but when you substitute t=2a+1 into that you do get s=(a+1)2, so it is a non-inductive invariant
termination condition
- \(t = 2 * \sqrt{n} + 1\)
if α is going to be invariant then it must be true before the loop begins
(1) = $$\alpha \Rightarrow ((\alpha|^1_{t})|^1_s)|^0_a$$
and it must be invariant through the loop
(2) = $$\alpha \Rightarrow ((\alpha|^{t+2}_{t})|^{s+t+2}_s)|^{a+1}_a$$
any formula which doesn't contain a, s, or t will trivially satisfy these conditions. lets list some α's
- a \(\geq\) 0
- s \(\geq\) 1 – this is not inductive because it relies on the value of t
- t \(\geq\) 1
- \(s \geq 1 \wedge t \geq 1\) – this is an inductive invariant, as its smaller than \(s \geq 1\)
- \(s \leq n + t + 1\)
- \(t \geq 1\)
let α be the strongest formula s.t. (1) + (2) are valid then α is the strongest inductive loop invariant
how do you know that a strongest formula exists? there could be an infinite number of α's which satisfy these properties, so only if you can write an infinite conjunction of these α's can you say that a strongest α must exist
now in terms of wp's
-
\(wp(while \, s \leq n \, \, do \, \, p \, \, end, \gamma)\)
-
β s.t.
- \(((\beta \wedge s \nleq n) \Rightarrow \gamma) \wedge ((\beta \wedge s \leq n) \Rightarrow wp(P, wp(L, \gamma)))\) where P stands for all three statements inside of our loop, and L is equal to the whole while loop, so we could make this into an infinite conjunction by continually replacing $L$ with the whole conjunction above with all of the variables updated with their deeper values
-
β s.t.
now looking at termination
control location l is visited finitely many times iff m(state(e)) keeps decreasing in a set where it is not possible to decrease forever
m(state(e)) means some measure m on the state
so for our program above the state can be the four-tuple
state = <a,s,t,n>
so if we let \(m() = N - s \in \{-N, \ldots, N\}\) then m will decrease with each loop iteration, and it can't decrease infinitely
some quick definitions
- given a set B partial ordering R on B is called well-formed iff it does not admit infinite chains of the form \(b_o R b_1 R b_2 R b_3 \ldots R b_{i+1}\), so < is well-formed on the natural numbers but < is not well formed on the integers
2010-02-25 Thu
An ordering is an anti-symmetric, transitive ordering.
an ordering is a total ordering if any two elements can be related to each other.
an ordering is strict if it is anti-reflexive
A strict partial ordering R on \(S(R \subseteq S \times S)\) is well-founded(Neothenan) iff R does not admit infinite chains of the form \(s_0 R s_1 R s_2 \ldots R s_i R s_{i+1}\), \(s_1 \ldots s_i \in R\)
for example our distance from 0 ordering on the integers
- |a| < |b| or |a| = |b| and a is neg. while b is pos.
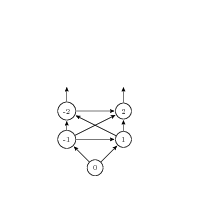
- termination
- requires a mapping M:p → s from program locations during execution to some state space S s.t. ∃ some well-founded relation R on S s.t. $$m(S^i_l) \, R \, m(S^{i+1}_l)$$
so, for example with our initial example where the loop terminates when y is no longer greater than 0, the set to which we map our states is the \(\mathbb{N}\), the relation R is <, and the measure of each state is the value of y
or with two nested loops
x = M y = N while y > 0 do y = y - 1 x = 1 while x < y do x = x + 1 end end puts "x=#{x} y=#{y}"
for the outer loop let m be the value of y and for the inner state let m be the difference between x and y, let both loop map to the naturals and in both cases let our relation be <.
so how do we get from knowing the constraints on an invariant of our program to guessing the invariant? We guess that the invariant will have the form of an equality in which every variable has degree less than or equal to 1.
$$Ax + By + Cz + Dxy + Eyz + Fxz + Gxyz = 0$$we then start applying our constraints(or substitutions) and we solve for these constants.
2010-03-02 Tue
cross orderings
what is the strongest possible ordering on \(R_{12} \subseteq R_1 \times R_2\) which is well founded. if \(R_{12}: (x,y) >_{12} (u,v)\) iff \(x >_1 u \vee (x,u) \notin R_1 \wedge y >_2 x\) which doesn't really work because of this counter example
(2, 1), (1, -2), (-2, -1), (-1, 2), (2, 1)
Collats's conjecture
while n != 1 do if n.even? then n = n / 2 else n = 3n + 1 end end puts n
slide-show
the rest of the class is from these slides
2010-03-04 Thu
the strongest ordering across two orderings
we can amend our previous ordering over (x,y) > (u,v)
- x > u, or
- x == u and y > v
now that we will never have a cycle we can say that given the well foundedness of our two previous orderings, each relation in our new ordering will be in one of the two previous and an infinite chain in the new ordering will imply an infinite chain the one of the two previous orderings, contradiction.
- \(R_1 \times R_2\) on \((x_1, y_2) < (x_1, y_3) < (x_1, y_4) < (x_2, y_1)\)
- \(R_1\) on \(x_1 < _ < _ < (x_2, y_1)\)
how do we order subsets and multisets
consider \(PF(S)\) the set of finite subsets of S
given an ordering \(>_s\) on the elements of S, how can we use it to relate elements of the power set
an element \(x \in A\) is maximal if \(\nexists y \in A\) s.t. \(y > x\), and same for minimal
some orderings
- just the size of the subsets – works but not very strong
- compare the maximal elements of each subset (assuming \(>_s\) is a total ordering)
- now for when \(>_s\) is a partial ordering we can do A is less than B iff \(A < B\) or \(\forall m \in (A - B)\), \(\exists n \in (B - A)\) s.t. \(n >_s m\)
- if you have an infinite DAG G divided into levels with a finite number of vertices at each level, s.t. each vertex at level i is related to a vertex at level i+1, then there must be an infinite path in G
- a set in which elements can be repeated
do define an ordering on multisets of S we can use the same ordering as above
using well founded orderings to show termination of complicated programs
you can use term re-writing (see slideshow iitd.pdf) to show that in infinite sequences of re-writes is not possible implying that a loop equivalent to those re-writes will terminate
2010-03-09 Tue
- some work from algebraic geometry can be used to help compute invariants
- see the "ideal theoretic" portions of the slideshow from last class
later…
- strongly connected component – a subgraph of a directed graph in which you can go from any node to any other node
slides available at cade09.pdf
2010-03-23 Tue
class started with a feedback form
there will not be term rewriting on the exam
control points in a program
(ref:p1) repeat (ref:p2) S1 (p3); if b_1 (ref:p4) then exit (ref:p5); (ref:p6) S2 (p7); if b_1 (ref:p8) then exit (ref:p9); (ref:p10) S3 (p11); until b (p12); end
relations between states
- \(P1 = \{Pre\}\)
- \(\{P2\} S1 \{P3\}\)
- \((P3 \wedge b_1) \Rightarrow P4\)
- \(P5 \Rightarrow P13\)
- \((P3 \wedge \not b_1) \Rightarrow P6\)
- \(\{P6\} S2 \{P7\}\)
- \((P7 \wedge b_2) \Rightarrow P8\)
- …
- \((P11 \wedge b) \Rightarrow P13\)
- \(P13 = \{Post\}\)
invariant at p2
weakest precondition
- leads to this verification condition using backwards semantics $$Pre \Rightarrow Post|^{x+z}_{x}$$
- and this verification condition using forward semantics $$\exists t (x := x+z|^t_x \wedge Pre|^t_x) \Rightarrow Post$$
some review of the last part of hw6
2010-03-30 Tue
Denotational Semantics
- denotational semantics
-
explicit state, and the meaning of a
program is a mathematical function
foundational basis is set-theory
program is a mathematical function
in our simple programming language we have
- expressions
- don't have side effects
- statements
- have side effects
there will be a larger differentiation between
- syntax
- programs
- semantics
-
functions
- semantic domains (e.g. \(\mathbb{N}\), Boolean values, functions on numbers, \(\mathbb{R}\), etc…)
- semantic values
- functions on those semantic domains
we will have an environment which is a mapping of identifiers to values, can be thought of as the memory or the state
standard notation – semantic equations
- \(\llbracket e \rrbracket\) is the meaning of the expression e
- \(\llbracket s \rrbracket\) is the meaning of the statement s
an expression is
- an identifier
- constant
- if 1 is a unary function symbol and e is an expression then 1e is an expression
- \(\llbracket x \rrbracket = st(x)\) where x is an identifier
- \(\llbracket c \rrbracket = \bar{c}\) where c is a constant
- \(\llbracket 1 e \rrbracket = \bar{1}\llbracket e \rrbracket\)
- \(\llbracket e_1 \circ e_2 \rrbracket = \llbracket e_1 \rrbracket \bar{o} \llbracket e_2 \rrbracket\)
- \(\llbracket x := e \rrbracket (st) = st'\) s.t. st' behaves exactly like st except on x, or more formally st(y)=st'(y) if y ≠ x
- function composition \(\llbracket s_1, s_2 \rrbracket = \llbracket s_1 \rrbracket \circ \llbracket s_2 \rrbracket\)
- \(\llbracket \text{if b then s1 else s2} \rrbracket = \llbracket b \rrbracket \rightarrow \llbracket s1 \rrbracket \, else \, \llbracket s2 \rrbracket\)
- \(\llbracket \text{while b do s end} \rrbracket = \llbracket b \rrbracket \rightarrow \llbracket \text{while b do s end} \rrbracket \circ \llbracket s \rrbracket \, else \, id\) where id is the identity function
simple language
we will focus on the simple language comprised of the following operators
- \(\circ\) function composition
- \(\text{if then else}\)
- \(\text{case}\)
- \(\text{recursion}\)
the only difficult part here is recursion which was dealt with by Scott and Strachey
examples
some definitions
- f(x) =def λ x . h1(h2(x)) which is equal to h1 \(\circ\) h2
- f(x) =def if x = \(\bar{0}\) then h1(x) else h2(x)
- f(x) =def if x = \(\bar{1}\) then \(\bar{1}\) else f(\(\bar{x} - \bar{1}\))
for each equation we'll reduce it to the set of those cases where the equation is true
- x=1 reduces to 1
- x2=2x reduces to 1
- x=2x reduces to 0
- 2x=2x+1 reduces to no solution
- x2=3x-2 reduces to 1 or 2
- x=x reduces to infinitely many solutions
for a program, we only want a single solution
when looking for a solution we always need to know
- solutions over what space
- what are the variables
finding the unique solution to a statement
f(x) =def if x = \(\bar{1}\) then \(\bar{1}\) else f(\(\bar{x} - \bar{1}\))
we need a unique solution for f(x)
we will say f(x)=1 is our unique solution to this statement
we can use induction, show for 0 then induce
we can prove uniqueness through contradiction, assume ∃ g(x) s.t. g(x) is also a solution.
2010-04-01 Thu
picking up from last time
λ st. if \(\llbracket b \rrbracket\) (st) then \(\llbracket \text{while b do s end} \rrbracket \circ \llbracket s \rrbracket\) (st) else st
= F(\(\llbracket \text{while b do s end} \rrbracket\))
F(x) = λ st. if \(\llbracket b \rrbracket\) (st) then \(x \circ \llbracket s \rrbracket\) (st) else st
how do we compute the fixed points of functions
- a fixed point of a function F:D->D is some \(v \in D\) s.t. f(v)=v
- f does not have a fixed point in D iff \(\nexists\) v s.t. f(v)=v
- if ∃ v1 and v2 in D s.t. v1 ≠ v2 and f(v1)=v1 and f(v2)=v2, then f has multiple fixed points
- let < be a partial ordering on D, then a fixed point v1 of f is strictly smaller than another fixed point v2 of f iff v2 < v1
- a fixed point v of f is minimal iff ∀ fixed points v' of f, either v=v' or v' is not < v
some examples
- h:N->N h(x)=0, 0 is the only fixed point of h
- h2:N->N h2(x)=x2, both 0 and 1 are fixed points. we can use the standard \(\geq\) as a partial ordering on these two fixed points
- S:N->N s(x)=x+1, this has no fixed points
- id:N->N id(x)=x, this has ∞ fixed points, depending on your ordering you could have ∞ minimal fixed points (e.g. if no elements are comparable)
stepping up
-
F1:[N->N]->[N->N], let D=[N->N]
F1(f) = f \(\circ\) f (ie. function composition)
a fixed point of this function could be id (the identity function), or any constant function
-
lets try to construct a function w/o a fixed point
F2(f) = succ . f
does ∃ g:N->N s.t \begin{eqnarray*} F_2(g) &=& g\\ succ(g(n)) &=& g(n)\\ g(n)+1 &=& g(n)\\ 1 &=& 0\\ &\lightning& \end{eqnarray*}
-
let h be a fixed point of F1, so F1(h) = λ n . h(h(n))
h = λ n.h(h(n))
information theoretic ordering
what elements of our domain have information, and \(\bot\) has no information
over the domain \(\mathbb{N} \cup \bot\) every element in \(\mathbb{N}\) has more information than bottom.
you could also use \(\top\) to force all elements into a lattice between \(\top\) and \(\bot\)
a lattice is a set and an ordering s.t. ∀ subsets ∃ a least upper bound and a greatest lower bound
a good example of a lattice is the power set of a set with respect to the subset ordering
if you have a typed language, you will have a \(\bot\) for each type, or a unique bottom in an untyped language
we'll let \(\mathbb{N}_{\bot}\) be the union of \(\mathbb{N}\) and \(\bot\)
a function is strict iff f(\(\bot\))=\(\bot\)
\(\bot\):$\mathbb{N}_{\bot}$->\(\mathbb{N}_{\bot}\) is the constantfunction on \(\bot\)
in some way, \(\bot\) is both "non-terminating computation" and "no information"
-
we have
F:\(D_{\bot}\) -> \(E_{\bot}\) and G:\(D_{\bot}\) -> \(E_{\bot}\)
F>G iff ∀ x ∈ \(D_{\bot}\) f(x)>g(x)
so the function \(\bot\) is the least function
so with \(\bot\) as a function, then every non-recursive definition has a least fixed point (namely \(\bot\))
building up a recursive function
F(h1) = λ x. if x=0 then 1 else h1(x-1) + h1(x-1)
- 0th approximation of h1: h10 = \(\bot\) is undefined everywhere
- 1st approximation of h1: F(h10) = λ x. if x=0 then 1 else h10(x-1) + h10(x-1) is undefined on \(\bot\), is 1 on 0, and is \(\bot\) everywhere else
- 2nd approximation of h1: F(h11) = λ x. if x=0 then 1 else h11(x-1) + h11(x-1) is defined on 0 and 1, but \(\bot\) everywhere else
- …
2010-04-06 Tue
A lattice is (D, ∧, ∨) with a partial ordering ⊂
- ∧ is the same as ∪ and is the greatest lower bound
- ∨ is the same as ∩ and is the least upper bound
the following must also be true
- a ∧ b = b ∧ a, (a ∧ b) ∧ c = a ∧ (b ∧ c)
- a ∨ b = b ∨ a, (a ∨ b) ∨ c = a ∨ (b ∨ c)
- a ∧ (a ∨ b) = a
- a ∨ (a ∧ b) = a
if S = {1,2,3} you get the following lattice
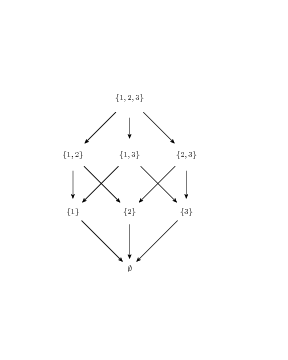
on \(\mathbb{N}\) gcd and lcm (least common multiple) are the meets and joins of the lattice defined by the "divides" operation.
- monotonic
- f:PO1 → PO2 is monotonic if x ≥1 y ⇒ f(x) ≥2 f(y)
- continuous
- f:PO1 → PO2 is continuous iff $$f(\vee(E)) = \vee_{x \in E}f(x)$$ where \(\vee(E)\) is the least upper bound of E
Questions
- does continuous -> monotonic
- how is \(\vee(E)\) a limit of the elements of E
continuing with more definitions
- chain
- a set E ⊆ D s.t. all element of E are comparable
- chain complete
- a lattice or a PoSet is complete iff every chain has a least upper bound in the lattice or set, this is only even a question in infinite sets, for example the chain of \(\mathbb{N}\) with the < relation, in which case the greatest element is not a natural number
- complete
- every subset has a least upper bound
with \(\mathbb{N}\) and < the least upper bound of a set of elements E is always max(E)
an easy example of a complete infinite set is the natural numbers between 0 and 1 inclusive.
bringing it all back to programming, each incremental approximation is a subsequent element in a chain, the limit of a chain is the meaning of the function
2010-04-08 Thu
Thanks to Ben Edwards for these notes.
- Last time we defined continuous function then stopped
- \(f: D \rightarrow D\) is continuous iff for every \(E \subset D\)
- $$\bigvee_{e \in E} f(e) = =f(\bigvee_{e \in C} e)$$
- So when do we have discontinuous funcitons(except in analysis)
- \(L=(P(N) \cup \{a\}, \subset, \cup, \cap)\)
- \(f: P(N) \cup \{a\} \rightarrow P(N) \cup \{a\}\)
- \(f(X) = \{X\) if $X$ is finite, \(X \cup \{a\}\) if $X$ is infinite
- This is monotonic
- $C$ us all the finite subsets of $N$
- The upper bound is $N$
- but f(least upper bound of N) has a in it
-
Tarski Knaster Theorem
- \(f:D \rightarrow D\)
- be a continus function on a complete partial ordere set with \(\bot\) as the least element of $D$
- then \(a=\cup_{n \geq 0} f^n(\bot)\) is the least fixed point of $f$.
- \(f^0(x) = x\) $fi+1(x) = f(fi(x))$
- The proof then logic programming context
- \(f(a) = f( \cup_{n \geq 0} f^n(\bot))\)
-
\(a = \cup_{n \geq 1} f^n(\bot) = f(\cup_{n \geq 0} f^n(\bot)) = f(a)\)
- By monotonicity and continuity
- So if we have a program
- The herbrand interpretation is a
- Our domain is \(D=P(HB)\)
- \(Tp:P(HB) \rightarrow P(HB)\)
- \(T_p\) is monotonic
-
Is it continuous
- Why is this fucker continuous
-
\(T_p(\cup_{i \geq 0} HI_i) \subset \cup_{i \geq 0} T_p(HI_i)\)
- \(HI_i \subset T_p(HI_i)\)
- We are basically done, as the defintion of \(T_p\) includes \(HI\) unioned with all ground substitutions
-
\(\cup_{i \geq 0} T_p(HI_i) \subset T_p(\cup_{i \geq 0} HI_i)\)
- \(HI_i \subset \cup_{i \geq 0} HI_i \Rightarrow T_p(HI_i) \subset TP(\cup HI_i)\) by monotonicity \(\forall i\). Booyah
- If it is the \(a = \cup_{i \geq 0} T_p^i(\emptyset)\) is the least fixed point, and this is the MEANING OF THE MODEL!
2010-04-13 Tue
presentation schedule
| Chayan, Ben G., Seth | |
| George, Thangthue, Roya | |
| Josh, Zhu, Wang | |
| Ben E., Scott, Eric |
review
- semantics of an expression \(\llbracket e \rrbracket (st) = val\) (a function from state to values)
- semantics of a statement \(\llbracket S \rrbracket (st) = st_1\) (a function from state to state)
so x++ is nasty because it is both a statement and an
expression, so it must return both a value and a new state.
so now every construct in our language which takes an expression must also treat that expression as a statement.
some interesting articles on non-interference properties of programming language features, ans also surface properties. these focused on how new features of programming languages affect other features – and in particular how this affects the parallelization of the function. (see Bob Tennant)
picking up from last time
Tp:P(HB) -> P(HB), the transformation program for a function p from the powerset of the Herbrand base to the powerset of the Herbrand base.
Tp(HI)={σ(H) : ∀ ground substitution σ, ∀ rule = (H :- L1, … Lk) ∈ P, if σ(Li) through σ(Lk) are all ∈ HI}
- monotonic HI1 ⊆ HI2 → Tp(HI1) ⊆ Tp(HI2)
-
continuous $$T_p(\cup_{i \geq 0}HI_i) = \cup_{i \geq 0}T_p(HI_i)$$,
we show this with ⊆ and ⊇
- ⊇: let x=σ(H) ∈ \(T_p(HI)\), then all the Li in the body of the rule with H are in HI, so they're all in \(\cup HI_i\), so they're all in \(T_p(\cup HI)\) -- this follows from the monotonicity of Tp
- ⊆: in (2) above all of the HIs are a chain and our ordering is ⊆, so the maximal element of all of the HIs contains every other HI and also all of the Li s in these other subsets
- is the above possible to prove w/o chains? NO it is not
2010-04-15 Thu
ASIDE: syntax, semantics and foundations of mathematics
- syntax
- well formed formulas
- semantics
- meanings of these formulas
there are also
- model theory
- validity, truth
- proof theory
- a theorem is a purely syntactic (algorithm check-able) finite object, provable with theorems
leading to
- soundness
- every theorem is true
- completeness
- every valid formula is provable with a theorem
Herbrand and Goedel, first order logic is complete
- Cantor's Theorem attempts to formalize sets, led to cardinality of ∞
- then Russle found a paradox in Cantor's theories of sets
- Hilbert began attempt to rigorize the foundations of mathematics, in 1900 Hilbert sets for a set of 25 problems facing mathematics including finding a formal system in which to ground all of mathematics
-
Goedel's incompleteness theorem: given any system of axioms Goedel
can create a formula s.t. you can't prove the formula or its
negation. This devastated Hilbert's program of rigidly formalizing
mathematics. He was schizophrenic
- Goedelization – any finite object can be represented as a number, so every formula, function, and theorem can be represented as a number
moving forward
- \bot
- program runs forever w/o terminating
- \top
- all of the information about the program, every input/output
back to looking at Tp over HIs
Tp(∪ HIi) ≠ ∪ Tp(HIi)
F:(N → N) → (N → N)
an infinite chain of functions
- λ x . \bot
- λ x . if x=0 then 0 else \bot
- λ x . if x=0 then 0 else (if x=1 then 1 else \bot)
- …
abstract interpretation
due to Patrick Cousot
- concrete domain lattice
- actual domain of a function
- abstract domain lattice
-
results of properties which want to show
are preserved by program (?)
-
example, parity lattice

- ordering of intervals ∅ ⊆ [1,1] ⊆ [1,3] ⊆ [-1,5] ⊆ [∞, infty]
-
example, parity lattice
function from variables to numbers
2010-04-20 Tue
non-monotonic reasoning, closed world assumptions, have relevance to AI
abstract interpretation
- turns out to be very useful in practice
- semantics on properties instead of on states
homomorphism: A mapping between algebras which preserves the meaning of the operations. So it must map the elements to elements and operations to operations. More formally a homomorphism is a map from S to T h:S → T, s.t. ∀ f,x,y ∈ S h(f(x,y))=\bar{f}(h(x),h(y)).
-
algebra is a set and some operators
- a = (S, {o,s,+,*})
- b = (T, {a,b,c,d})
each operation has some arity (e.g. unary function, binary, etc…)
if h is an onto mapping then it basically defines equivalence classes in S. x ∼ y iff h(x) = h(y), this may be called a homeomorphism
if a homomorphism is one-to-one and onto then it is an isomorphism
an example would be representing rational numbers as pairs of integers, then ∀ rational r there will be ∞ many pairs which are equivalent to r (e.g. 2 ∼ 2/1 and 4/2 and 6/3 etc…)
a decompiler is a homomorphism
- some examples w/homomorphisms
y := x + yif we only care about the sine of numbers
- A = (\(\mathbb{Z}\), {0, s, p, +})
- B = ({0, +, 1, ?}, {0b, sb, pb, +p})
our mapping is
- h(0) = 0
- h(x) = + if x > 0
- h(x) = - if x < 0
now applying some of these functions
-
s is successor
class s 0 + + + - ? -
p is predecessor
class p 0 - + ? - - -
minusb returns the negative
class - 0 0 + - - + -
plusb returns the same
class + 0 0 + + - - -
now adding and subtracting actual values
class + something - something 0 + - + + ? - ? -
In the above A would be the concrete domain and B would be our abstract domain.
- back to abstract interpretations
Concrete Domain Abstract Domain variable type integer sin (0, +, -) now we will have concrete and abstract lattices,
- CL = (C, \(\sqsubseteq_1\))
- AL = (A, \(\sqsubseteq_2\))
we will also have two operators
- C →αabstractization A
- P(C) ←γconcretization A
some things we can say about α and γ
- ∀ c ∈ C, α(c) will be its abstractization, then γ(α(c)) will return the equivalence class of c, so we know that {c} ⊆ γ(α(c))
- ∀ a ∈ A, γ(a) will return the equivalence class of a, so ∀ c ∈ γ(c), α(c) = a
- α and γ should be monotonic with respect to \(\sqsubseteq_1\) and \(\sqsubseteq_2\) so that they will be useful to us. Since \(\sqsubseteq_1\) and \(\sqsubseteq_2\) are operators in our algebras and α and γ are homomorphisms, they will both be monotonic because they must preserve all relations
what we've just defined is a Galois Connection
- analysis of Collat's program
A: while n \neq 1 do B: if even(n) then(C: n = n/2, D) else(E: n=3n+1, F) end Gwe can use a concrete lattice equal to the naturals and operators and an abstract lattice which tracks only sines. we can then perform analysis on the abstract lattice to make predictions about the sine of n in the Collat's program.
these lattices have the nice property of having finite depths, this means that it is possible to compute a fixed point
with infinite lattices (for examples intervals) we can use the widening operator to compress an infinite depth lattice into finite depth
2010-04-22 Thu
Program Synthesis – Ben G.
Program Synthesis – srivastava, gulwani, foster 2010
- high level program flow language
Program Slicing – Chayan
find what portions of a program are relevant to the value of a certain variable at a certain point.
recursively,
- line of interest
- select lines related to line
- recurse for every selected line
dynamic analysis used to limit the potentially over-large slices resulting from the above recursive solution
useful for fault localization, debugging, analyzing financial software
Order Sorted Unification – Seth
- using types to constrain unification
-
introduces an ordering on types
- often take GLB of two sorts during unification
- requires that types form a semi-lattice
2010-04-27 Tue
Semantic Aware Malware Detection – Roya Ensafi
signature vs. semantic classification/detection of malware
easy to change signature while preserving behavior
semantic aware malware detection 2005
similar def-use chains between example programs and templates used to identify malware
Functional Languages and circuits – George
- non-uniform computation
- boolean algebra
"reduceron" – is a uniform computer, where uniform means that the input size doesn't matter
circuit types
- combinational
- synchronous
- asynchronous
Situation calculus and BDI logic for agent based modeling – Thanaphon
- situational calculus
- first and second order logic, used for robot reasoning and planning. combine actions and situations
- BDI
- believe, decide, intention, central reasoner divorced from sensing and acting
frame problem and open-world problem
2010-04-29 Thu
Applications of Inductive Logic Programming – Josh Hecker
- induction ∩ logic programming
- repeatedly update a set of hypotheses using a set of inference rules until some stopping criteria
- inductive inference rules, i.e. induce the set G that would entail your set S, \(G \vDash S\)
applications
- program synthesis, given operators and positive examples it will induce the desired program
stochastic logic programming
- generalization of bayes nets and hidden Markov models
- consists of a set of clauses with probabilities
conclusion
- this isn't a practical way to synthesize programs
- ILP is used in learning the structure of some Bayesian networks
2010-05-04 Tue
Last round of Presentations
- I presented – schulte.non-von-neumann-computation.pdf
-
Scott Levy – Uncovering Software Defects using Loop Invariants
Demonstrated a means of working back from loop invariants to repair small bugs in imperative programs. Solving systems of equations for assignments for the loop invariants can result in a number of possible "fixes"
Related work
- Assertions [Clarke & Rosenblum 2006]
- Signposts
- Daikon [Ernst et al. 2006]
- Diduce [Hangal & Lam 2002]
- and Ben presented on the Analysis of Probabilistic programs using Axiomatic Semantics
2010-05-06 Thu
- some questions on abstract interpretation on the exam, but not much
- cumulative
- office hours Monday and Wednesday
Topics
lisp paper – λ the ultimate imperative
group theory
calculating least fixed points
taken from Email from Depak Computing fixed points, showing uniqueness and minimality of fixed points:
Given a recursive definition as a fixed point of a functional
F(f) (x) = body
in which body has free occurrences of f and x,
how do we determine whether a given function (table) is a fixed point of F?
Consider a function g which is a fixed point of F. What properties should this function satisfy?
F(g) = g, which
means that
g = bodyp
where bodyp is obtained from body by replacing all free occurrences of f by g.
Below, we assume that all functions and functionals are strict, i.e., if any argument is bottom, the result is bottom as well.
Let us start with problem 28.
1.
G(g)(x) = if x = 0 then 1 else x * g(x + 1).
Any fixed point, say h, of G, must satisfy:
G(h)(x) = if x = 0 then 1 else x * h(x + 1) = h(x).
I.e.,
h(0) = 1, h(x) = x * h(x + 1), x > 0.
Claim: Every fixed point h of G must satisfy the above properties.
Proof. Suppose there is a fixed point h' of G which does not satisfy the above equations.
case 1: h'(0) =/ 1:
given that h' is a fixed point,
G(h')(x) = if x = 0 then 1 else x * h'(x + 1) = h'(x)
h'(0) = 1
which is a contradiction.
case 2: there is an x0 > 0 such that h'(x0) =/ x0 * h(x0 + 1)
given that h' is a fixed point,
G(h')(x) = if x = 0 then 1 else x * h'(x + 1) = h'(x)
we have h'(x0) = x0 * h'(x0+1), which is a contradiction.
End of Proof.
Claim: h'(0) = 1, h'(x) = bottom, x > 0, is the least fixed point.
Proof: h' is a fixed point since it satisfies the above properties of all fixed points.
Any h'' smaller than h' must be such that h''(x) = bottom, but such a function does not satisfy the properties of a fixed point. So h' is the least function satisfying the properties of a fixed point.
Claim: There are other fixed points.
Proof: Besides h' in the previous example, there is another function which satisfy the above equations.
h''(0) = 1, h''(x) = 0, x > 0.
End of Proof
Claim: h' and h'' are the only two fixed points of the above functional.
Proof. h' and h'' are the only two functions satisfying the properties of all fixed points of the above functional. There is no other function satisfying h(x) = x * h(x + 1), x > 0.
End of Proof.
Let us consider a slight variation of problem 30. x - y = 0 if y >= x.
F(one, two) = ((lambda (x) (if (= 0 x ) x (+ 1 (two (- x 1))))), (lambda (x) (if (= 1 y ) y (- 2 (one (+ x 2))))))
Since the above are mutually recursive definitions, that is why they are written with multiple function variables as simultaneous arguments to F.
Let g and h be a fixed point of the above F, i.e.,
(g, h) = F(g, h),
which means:
- g(0) = 0
- g(x) = 1 + h(x - 1), x =/ 0
- h(1) = 1
- h(x) = 2 - g(x + 2), x =/ 1.
Claim: Any fixed point of F must satisfy the above equations.
Proof. It is easy to see that is the case.
A proof can be done by contradiction or by induction.
How many fixed points satisfy such equations?
Let us manipulate these equations a bit:
Using 2 and 3, we get
- g(2) = 1 + 1 = 2.
Using 5 and 4, gives
- h(0) = 2 - 2 = 0.
in addition, we also have:
g( x ) = 3 - g(x + 1), x > 2 h(x) = 1 - h(x + 1), x > 1
From these equations about characterizing fixed points, the least fixed point is obvious.
Are there any other fixed points?
Since every fixed point must satisfy the above two equations:
g(x) + g(x + 1) = 3, x > 2 h(x) + h(x+1) = 1, x > 1
One possibility is:
h(2k) = 0, h(2k + 1) = 1, k > 0,
Since we also have:
h(2 k) = 2 - g(2 k + 2), k > 0,
h(2 k + 1) = 2 - g(2 k + 3), k > 0,
it gives
g(2 k + 3) = 1, k > 0 g(2 k + 4) = 2,
another possibility is:
h(2k) = 1, h(2k + 1) = 0, k > 0,
which gives
g(2 k + 3) = 2, k > 0 g(2 k + 4) = 1,
It can be verified that these tables satisfy the above properties of all fixed points.
And, it can be verified that these are the only fixed points.
classic PL papers
quantifier-elimination … automatically generating inductive assertions
proving termination with multiset orderings
"fifth generation computing"
Japanese attempt at massively parallel logic computers
cardinality of sets – sizes of infinity
the size of the power set of any (even infinite) set is bigger than the size of the set
diagonalization
suppose ∃ $f$, a one-to-one mapping from s to P(s), it is not onto
consider the subset A ⊆ S, x ∈ A iff x ∉ f(x) -> ∃ y s.t. f(y) = A because then y ∈ A and y ∉ A
axiomatic semantics
related books
from George, Calculus of Computation.pdf
and then also, books.tar.bz2 with accompanying text…
In "Semantics with Applications", by Neilson and Neilson,
you might look at:
Chapter 1:
Has a good summary of operational, denotational, and axiomatic
semantics.
Chapter 2:
The way they write operational semantics is very similar to the way depak writes axiomatic
semantics. Just look at the way they write
,*if*, *skip*, and *while*.
Chapter 3: More Operational Semantics
Look at *abort*.
Chapter 5: Denotational Semantics
In the beginning, it has definitions for all the important syntax
in denotational semantics, like *if*, *skip*, *while*, sequencing, etc.
The "Fix point theory" section is really useful, up to the "continuous
functions".
Chapter 7: Program Analysis
Section 7.1 is useful and table 7.3 resembles what we did in class
on proving properties of programs in a restricted domain, like
{even,odd} or in the book, {+,-,0}.
Chapter 8: More on Program Analysis
This touches on the difference between forward and backward analysis
in denotational semantics, using a slightly different syntax than we
used in class. Ignore the 'security analysis'.
Chapter 9: Axiomatic Program Verification
See Section 9.2 and table 9.1 for the syntax we used in class for
axiomatic semantics. Pretty much from 9.2 on is useful.
In "The Calculus of Computation", by Bradley and Manna, you might
look at:
Chapter 12: Invariant Generation
Discusses invariants, strongest pre-condition, weakest post-condition,
abstract domains, and widening, all of which are course topics.
Unfortunately its all in different syntax than used in class.
P.S: thanks to Nate
Project – Non Von Neumann programming paradigms [5/5]
This project will investigate alternatives to traditional Von Neumann computer architectures and related imperative programming languages. A special focus will be placed upon the FP and FFP programming system described by Backus, the Propagator model as described by Sussman, and related issues of memory and processing structures.
DONE presentation notes
- add "a survey" to the title
- mention up front that this will review old non-VN paradigms, and how they are being echoed into the main stream
- put the relevant date on every page
- continually "touch base" with either a bounce back to the outline, or a bounce-back to a highlighted timeline
- take out the videos
- maybe hide some of the messiness of the history of the project -- don't do the propagator presentation – but add the code to a "backup" slide
Depak
- data flow
- is similar to cellular tree – no state outside of processing elements
- petri net
- is another topic people at MIT were into around this time.
DONE presentation
must send draft to Depak on the weekend before I present
- 20 minutes presentation
- 5 minutes questions
outline – Non-Von-Neumann Streams and Propagators
- history, VN
- related architecture and languages
- non-von architectures and languages
- Backus, FP and FFP
- Propagators
- examples of existing NVN hardware, and its potential for application to the above
stream
- clojure implementation
- background info
- merrimac – http://merrimac.stanford.edu/
- example applications
propagator
- memory layout
- background info
- clojure implementation
- example applications
topics
architectures / systems
- Cellular tree architecture: originated by Mago to run the functional language of Backus. fully binary tree the leaf cells of which correspond to program text.
-
the "jelly bean" machine, see
http://cva.stanford.edu/projects/j-machine/
- ran concurrent smalltalk
reduction machines
- reduceron
Graph reduction implemented on an FPGATI – Template Instantiation
- TI is the functional language
-
memories – can all be accessed in parallel
- template
- heap
- stack
-
compilation
- Haskell → yhc → TI
-
Haskell compiles to yhc, using church encodings the
dataandnumbericalvalues are encoded into λ-calculus
- A multi-processor reduction machine for user-defined reduction languages
reduction machine
- by-need computation
- machine language is called a reduction language
- state transition table generated automatically for a user to ensure harmonious interaction between processors
motivation for these machines
- new forms of programming
- architectures that utilize concurrency
- circuits that exploit VLSI
"substitutive" languages like lisp are inefficient on traditional hardware
is motivated by the need to increase the performance of computers, while noting that the natural physical laws place fundamental limitations on the performance increases obtainable from technology alone.
similar to machine designed by Berkling and Mago
- demand driven
- function is executed when its result is requested "lazy"
- data driven
- a function is executed when its inputs are present
design proposed in this paper
Each processor in the machine operates in parallel on the expression being evaluated, attempting to find a reducible sub-expression. The operation of each processor is controlled by a swappable, user-defined, state transition table.
reduction machine replace sub-expressions with other expressions of the same meaning until a constant expression is reached, like solving an equation by replacing
1 + 8with9. The sub-expressions may be solved in parallel.fully bracketed expressions (like parens in lisp) allow parallelization whenever multiple bracketed expressions are reached simultaneously.
It consists essentially of three major parts, (i) a common memory containing the definitions, (ii) a set of identical, asynchronous, processing units (PU), and (iii) a large segmented shift register containing the expression to be evaluated. This shift register comprises a number of double ended queues (DEQ) containing the parts of the expression being traversed, and a backing store to hold surplus parts of the expression. Each processor has direct access to the common memory and two double ended queues.


basic idea is that expressions are divided among processors each of which reduces its part of the expression in parallel. Big plans for hardware implementations which either never came or didn't last.
main stuff
constraint programming
- 10.1.1.91.3166.pdf – dissertation on constraint programming
- constraints_96.pdf – from http://mozart-oz.org
- 10.1.1.1.9348.pdf – comparison of some constraint propagation engines
reduction machines
-
also, look for a copy of
Mago, G.A. A network of microprocessors to execute reduction languages. To appear in Int. J. Comptr. and Inform. Sci.
- p121-treleaven.pdf – p121-treleaven.txt – (see treleaven-paper)
- p890-sanati-mehrizy.pdf
- look at these Springerlink articles
- p105-sullivan.pdf
functional logic programming
-
also look at
I do not see how other resources are going to be helpful. Perhaps you should do a literature search on functional/logic programming. Also, see the recent issue of CACM.
- propagator springerlink article
- logic programming in clojure
I just posted a new tutorial about doing logic programming in Clojure. It makes use of the mini-Kanren port to Clojure I did last year. Its intended to reduce the learning curve when reading "The Reasoned Schemer", which is an excellent book. http://intensivesystems.net/tutorials/logic_prog.html Jim
- Multi-paradigm Declarative Languages – Michael Hanus
- declarative programming languages are higher level and result in more reliable and maintainable programs
- they describe the what of a program rather than spelling out the how
3 types of declarative programming languages
- functional descendants of the λ-calculus
- logic based on a subset of predicate logic
- constraint specification of constraints and appropriate combinators – often embedded in other languages
Stream/Data-flow programming
- wiki/Dataflowarchitecture, Stream_processing, Dataflow_programming, Flow-based_programming
- Stanford's merrimac streaming supercomputer, see
misc
- events vs. threads usenix:events-vs-threads
- parallelization (see Bob Tennant)
- history of Haskell – history-of-haskell.pdf
- why functional programming matters
- reduceron.pdf
- system F
- http://www.dnull.com/cpu/
- Non Von-Neumann computation – H. Riley 1987
http://www.csupomona.edu/~hnriley/www/VonN.html-
language directed design – McKeenan 1961, stored values are typed
(e.g. integer, float, char etc…)
One is what Myers calls "self-identifying data," or what McKeeman
-
functional programs operating on entire structures rather than on
simple words – Backus 1978, Eisenbach 1987
Another approach aims at avoiding the von Neumann bottleneck by the use of programs that operate on structures or conceptual units rather than on words. Functions are defined without naming any data, then these functions are combined to produce a program. Such a functional approach began with LISP (1961), but had to be forced into a conventional hardware-software environment. New functional programming architectures may be developed from the ground up [Backus 1978, Eisenbach 1987].
-
data flow – not single sequence of actions of program, but rather
only limits on sequencing of events is the dependencies between data
A third proposal aims at replacing the notion of defining computation in terms of a sequence of discrete operations [Sharp 1985]. This model, deeply rooted in the von Neumann tradition, sees a program in terms of an orderly execution of instructions as set forth by the program. The programmar defines the order in which operations will take place, and the program counter follows this order as the control executes the instructions. This "control flow" approach would be replaced by a "data flow" model in which the operations are executed in an order resulting only from the interdependencies of the data. This is a newer idea, dating only from the early 1970s.
-
language directed design – McKeenan 1961, stored values are typed
(e.g. integer, float, char etc…)
Non Von Neumann Languages
the take homes here are many (Function Level FLProject.pdf) and array programming languages
APL
http://en.wikipedia.org/wiki/APL_programming_language
probably the most interesting
- its own special non-ascii characters
- in 19802 the Analogic Corporation developed The APL Machine
- runs on .NET visual studio
- recently gained object oriented support
- has gained support for λ-expressions dfns.pdf
-
Conway's game of life in one line of APL code is described here

many programs are "one liners", this was a benefit back in the days of having to halt a program to read the next line from disk.
terms/topics
MIMD Multiple instruction stream, Multiple Data stream languages
ZISC
zero instruction set computer, somehow does pattern matching instead of machine code instructions
http://en.wikipedia.org/wiki/ZISC
application http://www.lsmarketing.com/LSMFiles/9809-ai1.htm
NISC
No instruction set computer, all operation scheduling and hazard handling are done by the compiler
FPGA
- in use http://www.celoxica.com/technology/technology.html
- http://en.wikipedia.org/wiki/Handel-C – language for FPGA
DONE proposal
After exchanging some emails with me, you will zero in on the topic, firming about what you plan to do. After that you will write a 1-page max proposal about the details, time line, etc. The deadline for this is April 9, but I am hoping that I get the proposal from you sooner.
proposal
I plan to pursue the following in completion of my semester project.
- Continue to read papers about Non Von Neumann style programming systems (e.g. propagators) which allow for new memory and processor organization and for concurrent processing.
- Extend the propagator system described in Sussman's paper so that it supports parallel execution.
- Find a problem which is amenable to this sort of programming system, and demonstrate the implementation of an elegant solution.
At the completion of this project I expect to deliver the following.
- an implementation of the concurrent propagator system
- a paper discussion various non Von Neumann programming models
- a solution to a programming problem demonstrating some of the strengths of these different programming models
- Clojure
Clojure 2 is a lisp dialect that is designed from the ground up for concurrent programming 3. It has a number of features directed towards this goal including- automatic parallelism
- synchronization primitives around all mutable objects
- immutable data structures
- a Software Transactional Memory System (STM)
It is freely available, open source, runs on the Java Virtual Machine, and I am already very familiar with it. Using this language should make parallelization of Sussman's propagation system (which is already implemented in lisp) a fairly easy implementation project (on the order of a weekends worth of work).
DONE Concurrent propagator in Clojure
Can programming be liberated from the Von Neumann style – John Backus
backus_turingaward_lecture.pdf backus_turingaward_lecture.txt
This looks great.
The purpose of this article is twofold; first, to suggest that basic defects in the framework of conventional languages make their expressive weakness and their cancerous growth inevitable, and second, to suggest some alternate avenues of exploration toward the design of new kinds of languages.
Complains about the bloat and "cancerous growth" of traditional imperative programming languages, which are tied to the Von Neumann model of computation – state / big global memory.
Crude high-level programming languages classification
| foundations | storage/history | code clarity | |
|---|---|---|---|
| simple operational | simple | unclear | |
| turing machine, automata | mathematically useful | yes | conceptually not useful |
| applicative | simple | clear | |
| lisp, lambda calc | mathematically useful | no | conceptually useful |
| Von Neumann | complex, bulky | clear | |
| conventional, C | not useful | yes | conceptually not useful |
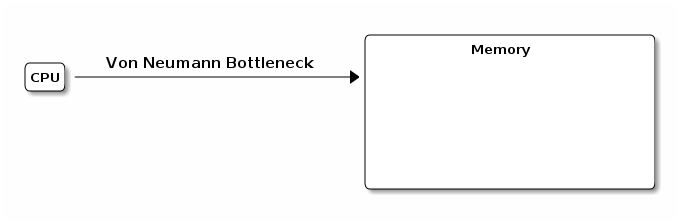
- Von Neumann model
-
CPU and memory connected by a tube
 splits programming into the world of
splits programming into the world of
- expressions
- clean mathematical, right side of assignment statements
- statements
- assignment
- comparison of Von Neumann and functional program
- many good points about the extendability of functional program, and the degree to which Von Neumann programs spend their effort manipulating an invisible state.
- framework vs. changeable parts
- Von Neumann languages require large baroque frameworks which admit few changeable parts
- mathematical properties
-
again Von Neumann sucks
- Axiomatic Semantics
-
is precise way of stating all the
assignments, predicates, etc… of imperative languages.
this type of analysis is only successful when
addition to their ingenuity: First, the game is restricted to small, weak subsets of full von Neumann languages that have states vastly simpler than real ones. Second, the new playing field (predicates and their transforma- tions) is richer, more orderly and effective than the old (states and their transformations). But restricting the
- Denotational Semantics
- more powerful, more elegant, again only for functional languages
Alternatives – now that we're done trashing traditional imperative languages lets look at some alternative programming languages. specifically applicative state transition (AST) systems involving the following four elements
- (FP) informal functional programming w/o variables, simple based on combining forms to build programs
- an algebra of functional programs
- (FFP) formal functional programming, extends FP above combined with the algebra of programs
- applicative state transition (AST) system
over lambda-calculus
with unrestricted freedom comes chaos. If one constantly invents new combining forms to suit the occasion, as one can in the lambda calculus, one will not become familiar with the style or useful properties of the few combining forms that are adequate for all purposes. Just as structured programming eschews many control statements to obtain programs with simpler structure, better properties, and uniform methods for understanding their behavior, so functional programming eschews the lambda expression, substitution, and multiple function types. It thereby achieves programs built with familiar functional forms with known useful properties. These programs are so structured that their behavior can often be understood and proven by mechanical use of algebraic techniques
FP systems offer an escape from conventional word- at-a-time programming to a degree greater even than APL (12) (the most successful attack on the problem to date within the von Neumann framework) because they provide a more powerful set of functional forms within a unified world of expressions. They offer the opportunity to develop higher level techniques for thinking about, manipulating, and writing programs.
proving properties of programs, algebra of programs
One advantage of this algebra over other proof tech- niques is that the programmar can use his programming language as the language for deriving proofs, rather than having to state proofs in a separate logical system that merely talks about his programs.
while straight FP allows for combination of functional primitives, FFP allows these composed functions to be named and added to the library of functions extending the language.
in other words objects can represent functions in FFP systems.
-
Applicative State Transition (AST) systems
The possibility of large, powerful transformations of the state S by function application, S–>f:'S, is in fact inconceivable in the von Neumann–cable and protocol–context
Whenever AST systems read state they either
- read just a function definition from the state
- read the whole state
the only way to change state is to read the whole state, apply a function (FFP), then write the entire state. the structure of a state is always that of a sequence.
makes a big deal about not naming the arguments to functions (variables), but then provides small functions which pull information from memory and which look just like variables. I wonder what the benefit is here, Backus seems to think there is one
names as functions may be one of their more important weaknesses. In any case, the ability to use names as functions and stores as objects may turn out to be a useful and important programming concept, one which should be thoroughly explored.
false starts
CANCELED Robert Kowalski
-
State "CANCELED" from ""
nope, found something better
also, Rules.pdf
it looks like wiki:RobertKowalski has done some interesting work with generalizations of the traditional logic programming constructs bringing them to multiple agent systems, as well as showing that they are special cases of assumption-based argumentation.
See
- multi-agent systems in lpmas.pdf and recon-abst.pdf
- assumption-based argumentation in arg-def.ps.gz and ABAfinal.pdf
- parallel logic programming at http://www.cs.nmsu.edu/~epontell/adventure/node12.html
CANCELED generate and test programming
-
State "CANCELED" from "TODO"
probably not - live(real-time) test integration
- constraint programming
- search based programming
somewhere in here is something interesting
Terms
Definitions of some terms from this class
Basics / Misc
- formalist
- (platonic ideals are not real) everything is syntax -- there is nothing more than symbol manipulation
- syntax
- symbols, grammar: rules specifying valid program text
- semantics
- meaning
- Backus Naur Form (BNF)
- define languages through production rules
- language
- A language consists of an alphabet Σ={a,b,c}, and all finite strings taken from Σ
- formal grammar
-
is a collection (N, Σ, P) where
- N is the set of all non-terminating symbols
- Σ is the set of all terminating symbols
- P is the set of all production rules
- context free grammar
- every production rule is of the form V → w, where V ∈ N (i.e. is a non-terminal) and w is a string of terminals and/or non-terminals
- regular languages
-
a formal grammar in which every production rule
is of one of the following forms
- B → a : where B ∈ N, and a ∈ Σ
- B → aC : where B,C ∈ N, and a ∈ Σ – for right regular grammers
- B → Ca : where B,C ∈ N, and a ∈ Σ – for left regular grammers
- B → σ : where B ∈ N, and σ=∅ (the empty string)
- Turing language
- or "type 0" language are any collection of terminals and non-terminals
- multiset
- a set in which elements can be repeated
- expressions
- don't have side effects
- statements
- have side effects
λ-calculus rules
- β-rule
- evaluates an application of an abstraction to an expression. ((λ (x) e) e2), replace all free occurrences of x in e with e2
- α-rule
- expressions are equal up to universal uniform variable renaming, and the α-rule allows you to rename bound formal parameters
- η-rule
- (λ (x) (e x)) -> e
Logic Programming
- literal
- is an atom or its negation
- relations
- are named by predicate symbols
- terms
-
argument to predicate symbols
- variable
- constant
- functor applied to a term
- atom
- is a predicate symbol applied on terms
- query
- a function call, a set of initial states and you want to see if and what satisfies them, a predicate symbol with a set of terms
- functors
-
are the basic functions in the language (e.g.
cons) - ground term
- a term w/o variables
- clause
- disjunction of a finite set of literals (∨'d together)
- clause
- disjunction of a finite set of literals (∨'d together)
- horn clause
- most logic programming only deals with Horn clauses, these are clauses in which at most one literal is positive -- e.g. ¬ p ∨ ¬ q ∨ … ¬ t ∨ u, or written as an implication, (p ∨ q ∨ t) → u
- logic program
- the conjunction of a finite set of Horn clauses
- unifier
- a set of substitutions of the variables in a system of equations which makes them all equal
- most general unifier
- a set of substitutions of the variables in a system of equations which includes all other valid variable assignments
- Herbrand Universe
- all possible ground terms which can be constructed using symbols (or functor-symbols) in the program -- the objects between which relations are being defined. This will be finite if there are no function symbols and infinite if there are any function symbols
- Herbrand Base
- every possible application of our relational systems against the elements of our Herbrand Universe -- regardless of whether the relation holds or is true over those elements
- Herbrand Interpretation
- is any subset of the Herbrand Base
- herbrand model
- the minimal ⊆ of the herbrand base in which all clauses are valid – a small note on clause validity. A clause (H :- L1, …, Lk) is valid iff all ground substitutions on L1 through Lk are in the interpretation, and ground substitutions on H are also in the model.
- Operational Semantics
- the minimal Herbrand Model, or the intersection of all Herbrand Models for a program
- herbrand universe
- all possible ground terms which can be constructed using symbols (or functor-symbols) in the program – the objects between which relations are being defined. This will be finite if there are no function symbols and infinite if there are any function symbols
Semantics and analysis
- precondition
- property about the state before the execution of some imperative action
- postcondition
- property about the state after the execution of some imperative action. can be considered a subset of the set of possible states containing only those for which the property is true.
- strongest postcondition
- given an initial state, and some imperative action, the strongest postcondition, is the smallest subset of possible states after the execution of the imperative action against the state.
- weakest precondition
- given a post condition and some imperative action, the weakest precondition is the largest number of possible states which could be transformed by the imperative action into the post condition.
- invariant
- a property which remains true at multiple points in a program (e.g. at each iteration of a loop, or throughout an entire program)
- hoare triple
- ({precondition}, imperative action, {postcondition})
- verification condition
- a pre or post condition with the appropriate axiom or substitution applied for a given statement
- well founded ordering
- a partial ordering which does not admit ∞ chains
- static analysis
- tries to prove some easy properties about programs through analysis of the program w/o execution
- dynamic analysis
- analysis of a program which involves examining the program during execution
- total correctness
- given an input spec then both the program terminates and the output spec is satisfied
- partial correctness
- given an input spec and assuming the program terminates then the output spec is satisfied
- termination
- requires a mapping M:p → s from program locations during execution to some state space S s.t. ∃ some well-founded relation ⊆R on S s.t. $$m(S^i_l) \, \subseteq_R \, m(S^{i+1}_l)$$
- denotational semantics
-
explicit state, and the meaning of a
program is a mathematical function
foundational basis is set-theory
program is a mathematical function
Math stuffs
- monotonic
- f:PO1 → PO2 is monotonic if x ≥1 y ⇒ f(x) ≥2 f(y)
- continuous
- f:PO1 → PO2 is continuous iff $$f(\sqcup(E)) = \sqcup_{x \in E}f(x)$$ where \(\sqcup(E)\) is the least upper bound of E
- chain
- a set E ⊆ D s.t. all element of E are comparable
- chain complete
- a lattice or a PoSet is complete iff every chain has a least upper bound in the lattice or set, this is only even a question in infinite sets, for example the chain of \(\mathbb{N}\) with the < relation, in which case the greatest element is not a natural number
- complete
- every subset has a least upper bound
- soundness
- every theorem is true
- completeness
- every valid formula is provable with a theorem
- \(\bot\)
- program runs forever w/o terminating
- \(\top\)
- all of the information about the program, every input/output
Theorems and Lemmas
- Konig's Lemma
- if you have an infinite DAG G divided into levels with a finite number of vertices at each level, s.t. each vertex at level i is related to a vertex at level i+1, then there must be an infinite path in G
Footnotes:
1 calls "typed storage." In the von Neumann computer, the instructions themselves must determine whether a set of bits is operated upon as an integer, real, character, or other data type. With typed storage, each operand carries with it in memory some bits to identify its type. Then the computer needs only one ADD operation, for example, (which is all we see in a higher level language), and the hardware determines whether to perform an integer add, floating point add, double precision, complex, or whatever it might be. More expensive hardware, to be sure, but greatly simplified (and shorter) programs. McKeeman first proposed such "language directed" design in 1961. Some computers have taken steps in this direction of high-level language architecture, becoming "slightly" non-von Neumann.
1 FOOTNOTE DEFINITION NOT FOUND: 1967