

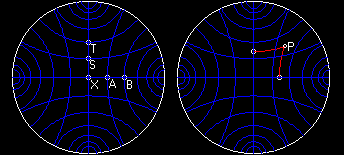
La figura mostra 24 rette iperboliche che possono essere utilizzate per definire un sistema di coordinate nel piano iperbolico. Il punto X si trova nell'origine di questo sistema di coordinate e le rette orizzontali e verticali di figura, che si intersecano in X, individuano gli assi x e y. Gli assi dividono il piano iperbolico in quattro quadranti analoghi ai quadranti del piano cartesiano in geometria euclidea. In figura vediamo una serie di rette parallele perpendicolari agli assi e distanti tra loro 0,5 unità di misura. La lunghezza del segmenti XA = AB = XS = ST = 0,5 unità di misura. Nel piano cartesiano euclideo le coordinate di un punto nel primo quadrante sono definite come coppie ordinate (x,y) dove x indica la distanza del punto dall'asse x e y la distanza del punto dall'asse delle y. Punti nel secondo, terzo e quarto quadrante hanno coordinate rispettivamente (-x,y), (-x,-y) e (x,-y). Possiamo applicare la stessa definizione in geometria iperbolica, in modo che ogni punto del piano è univocamente determinato da una coppia di coordinate. Nonostante la definizione delle coordinate in geometria iperbolica ricalchi la definizione data in geometria euclidea non è possibile ricorrere al metodo euclideo per determinare la posizione di un punto nel piano iperbolico. Ad esempio, in geometria euclidea, per determinare la posizione del punto P(1,1) possiamo tracciare prima la perpendicolare all'asse x a partire dal punto dell'asse x che dista 1 dall'origine e quindi tracciare la perpendicolare all'asse y passante per il punto dell'asse y che dista sempre 1 dall'origine. Intersecando le perpendicolari si ottiene il punto P. Questo procedimento tuttavia non funziona in geometria iperbolica in quanto le rette perpendicolari all'asse x e y, passanti rispettivamente per i punti B e T dell'asse x e y posti a distanza unitaria dall'origine, non si intersecano! Sembra allora che il punto (1,1) risulti indefinito in geometria iperbolica; in realtà il punto (1,1) è ben definito come si vede in figura. La lunghezze dei segmenti giacenti sulle perpendicolari da P all'asse x e da P all'asse y sono unitarie, mentre non sono unitarie le distanze dei piedi delle perpendicolari dall'origine degli assi. La loro distanza è infatti 0,7 unità di misura.
Il sistema di coordinate che abbiamo definito induce una corrispondenza biunivoca tra punti del piano iperbolico e coppie ordinate di numeri.
 Pagina Iniziale
Pagina Iniziale
 Successivo - Modelli del Disco e del Semipiano di Poincaré
Successivo - Modelli del Disco e del Semipiano di Poincaré
Copyright©: Joel Castellanos, 1994-2002