La Pseudosfera

La geometria sferica piana si rappresenta in modo adeguato lavorando sulla superficie di una sfera. In modo del tutto analogo la geometria iperbolica piana si rappresenta in modo adeguato lavorando sulla superficie di una pseudosfera. Ma che cos'è una pseudosfera?

Una pseudosfera, come una sfera, può essere pensata come una superficie bidimensionale. In un certo senso possiamo dire che la sfera è "più piccola" del piano in quanto essa si chiude su se stessa ed è limitata mentre il piano è illimitato. Al contrario la pseudosfera è "più grande" del piano. Sia il piano che la pseudosfera sono infiniti ma la pseudosfera è più ricca di "stanze" del piano. Possiamo anche dire che la pseudosfera ha un grado di infinità maggiore del piano.

Dal momento che la pseudosfera è più grande del piano essa è difficilmente rappresentabile attraverso le costruzioni della geometria euclidea usuale. Tuttavia esiste un trucco per costringere la pseudosfera ad adattarsi in un cerchio e questo trucco prende il nome di "Modello del disco di Poincaré della geometria iperbolica". Le Figure A, B e C sottostanti sono immagini di schermate del software NonEuclid. In ciascuna figura la circonferenza in bianco rappresenta la Circonferenza Limite della pseudosfera. Per costringere la pseudosfera ad abitare gli angusti limiti del disco è necessario distorcerla; tuttavia gli effetti della distorsione che si produce sono davvero gradevoli! Oltre a questo il modello del disco di Poincaré è geometricamente equivalente alla pseudosfera. In altri termini ogni teorema valido per il modello di Poincaré è valido anche sulla pseudosfera.

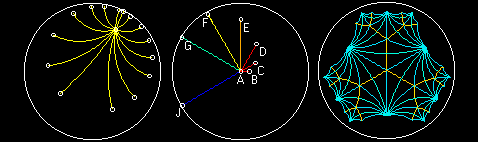
Figura 3a: Segmenti congruenti con un punto in comune.
Figura 3b: Segmenti di lunghezza 0.25, 0.5, 1.0, 2.0, 4.0, 8.0 e 16.0.
Figura 3c: Tassellazione con Triangoli congruenti.

Quando un punto si avvicina alla circonferenza limite la sua distanza dal centro tende all'infinito. La Figura-3a mostra un insieme a di segmenti di lunghezza 3 unità di misura. Osserviamo che più ci avviciniamo alla circonferenza limite più un segmento appare "corto". L'insieme di questi segmenti si può pensare come un insiemi di raggi di una circonferenza in quanto hanno tutti la medesima lunghezza ed un punto in comune.

I segmenti di Figura-3b hanno in comune il centro della circonferenza limite. Il segmento AB ha lunghezza pari a 0,25 unità. Il segmento AC ha lunghezza pari a 0,5 unità. Muovendosi in senso orario ogni segmento ha lunghezza doppia rispetto al precedente. Gli ultimi due segmenti (AG e AJ) appaiono lunghi uguali mentre AJ (che supera AG di mezzo pixel) misura il doppio di AG!

In relazione alla risoluzione del tuo monitor noterai che usando NonEuclid per disegnare dei punti il cursore non riesce a spostarsi più di dieci unità di misura dal centro del disco senza uscire dal modello. Ciò è dovuto al fatto che lavorando sullo schermo di un calcolatore si ha un limite dovuto alla granularità del singolo pixel. In ogni caso la distanza tra l'ultimo punto disegnato dal calcolatore e la circonferenza limite è infinita.

Anche se è impossibile rappresentare nello spazio e in modo continuo tutta la pseudosfera possiamo rappresentarne delle parti ricorrendo a diverse superfici limitate. Attraverso l'analisi di queste parti possiamo formarci un'idea dell'intera superficie. Le Figure 3d e 3f sono dovute a David Povilaitis e sono tratte dal testo di Rudy Rucker "The Fourth Dimension".

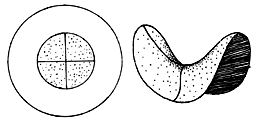
Figura 3d - Una sezione circolare di pseudosfera è rappresentata da una sella. [Rucker-84]

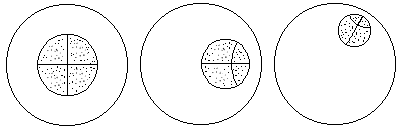
Figura 3e - Settori circolari di uguale raggio che sezionano parti diverse della pseudosfera individuano selle uguali.

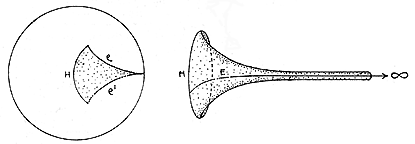
Figura 3f - Un settore che seziona la pseudosfera fino all'infinito è rappresentato da una tromba. [Rucker-84]

Pagina Iniziale
Successivo - Parallelismo