

2.1 Geometria e Fisica
L'idea che lo spazio geometrico possa avere diverse "forme" possibili è stata introdotta in matematica Bernard Riemann nella prima metà dell'Ottocento. Nella geometria di Riemann la forma dello spazio è definita attraverso la sua curvatura. E' interessante notare come le idee di Riemann trovino una notevole applicazione nella fisica relativistica. Nella teoria della Relatività Generale, elaborata da Einstein nel 1915, il concetto fisico di gravità viene legato a quello di curvatura di uno spazio quadridimensionale (spazio-tempo) secondo le seguenti idee:
Uno dei campi in cui le idee relativistiche hanno esercitato maggiore influenza è senza dubbio quello cosmologico. L'immagine che ci si forma studiando i modelli cosmologici moderni è che l'universo abbia quattro dimensioni e che, in relazione alla distribuzione di materia ipotizzata, esso sia caratterizzato da una certa curvatura. Questa immagine è necessariamente astratta in quanto domande del tipo quale sia la quarta direzione, se sia in alto o in basso, a destra o a sinistra sono del tutto prive di significato.
2.2 L'orbita di Mercurio
La distanza della Terra dal Sole risulta troppo piccola per permettere, anche agli strumenti più sensibili, di percepire gli effetti fisici dovuti alla curvatura dello spazio. Tuttavia gli effetti di curvatura risultano significativi nello studio del moto di Mercurio. L'idea è che Mercurio, che è il pianeta più vicino al Sole, risenta maggiormente degli effetti di curvatura generati dalla notevole massa solare. Le predizioni, eseguite con la teoria classica delle perturbazioni, della posizione del suo perielio (punto in cui il pianeta si trova più vicino al Sole), valutate su lunghe scale di tempo, non concordano con i dati sperimentali. Se tuttavia si includono nei calcoli le correzioni dovute agli effetti di curvatura relativistica si riesce a raggiungere un soddisfacente accordo tra teoria e osservazione.
2.3 Flatlandia
La "visualizzazione" dello spazio a quattro dimensioni, di cui abbiamo accennato in precedenza, non è immediata. Per comprendere come si possa affrontare ci riferiamo a quanto contenuto in un romanzo che il maestro inglese Edwin Abbott scrisse nel 1884. Nel romanzo si parla di un immaginario mondo bidimensionale chiamato Flatlandia. Flatlandia è abitato da creature che scivolano; possiamo pensare a monete su un tavolo o a zone colorate su una bolla di sapone. La storia è centrata sulle avventure di Quadrato, il più famoso abitante di Flatlandia, e sul suo percorso verso la comprensione della terza dimensione. Pensando a Quadrato e alle sue difficoltà nella comprensione della terza dimensione possiamo farci un'idea delle nostre difficoltà nel trattare la quarta dimensione. All'inizio della storia Quadrato e la moglie vivono confortevolmente nella pace della loro casa quando all'improvviso una voce proveniente da un luogo sconosciuto si rivolge loro. Un istante dopo, nella loro abitazione ermeticamente chiusa, appare una circonferenza. Si tratta di Sfera che viene per insegnare a Quadrato come affrontare la terza dimensione:
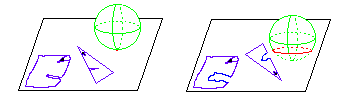
"Io non sono una Figura piana, ma un Solido. Voi mi chiamate Circolo; ma in realtà io non sono un Circolo, bensì un numero infinito di Circoli, di dimensioni varianti da un Punto a un circolo di venticinque centimetri di diametro, posti l'uno sull'altro. Quando io interseco il vostro piano come sto facendo adesso, opero nel vostro piano una sezione che voi assai appropriatamente chiamate Circolo. Perché se una Sfera (è così che mi chiamo al mio paese) si manifesta a un abitante della Flatlandia, non può manifestarsi che come Circolo." [Abbott-1884]
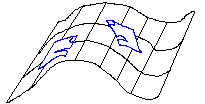
Flatlandia non è necessariamente un luogo piatto. La coppia di abitanti di Flatlandia di figura vive in uno spazio bidimensionale che, in tre dimensioni, appare curvo. Gli abitanti di Flatlandia non percepiscono la curvatura dello spazio in cui vivono in quanto tutti gli oggetti circostanti, compresi i loro corpi, sono curvi come la superficie bidimensionale che li ospita.
2.4 La nostra Terra
Il protendersi del nostro universo nella quarta dimensione è diverso su tre diversi ordini di scala: su piccola scala la curvatura è determinata da ciascuna particella subatomica; su scala intermedia la curvatura è determinata dalla gravità esercitata dalle galassie, dalle stelle, dai buchi neri e dai corpi celesti; su larga scala la curvatura è determinata dalla totalità di materia e energia presente nello spazio. Per chiarire che cosa si intende per diversa "scala di curvatura" consideriamo il seguente esempio: su larga scala diciamo che la Terra è curva ed ha forma sferica con un leggero schiacciamento ai Poli; su media scala, ad esempio quando possiamo vedere da una montagna l'orizzonte, la Terra appare piatta. Su piccola scala, quando ci guardiamo intorno, la curvatura della Terra varia da punto a punto a causa della presenza di rilievi e di avvallamenti di ogni genere.
 Pagina Iniziale
Pagina Iniziale
 Successivo - La Pseudosfera
Successivo - La Pseudosfera
Copyright©: Joel Castellanos, 1994-2001