

1 Area del Triangolo
In geometria euclidea l'area A di un triangolo si determina moltiplicando la lunghezza b di un qualsiasi suo lato per la lunghezza h della corrispondente altezza e dividendo il prodotto per due (A=bh/2). L'esempio sottostante mostra la costruzione delle altezze di un triangolo in geometria iperbolica.

Figure 6.1: Altezze di un Triangolo
Il triangolo ABC è scaleno. I segmenti AX, BY e CZ individuano le tre altezze del triangolo ABC. Osserviamo che, come in geometria euclidea le tre altezze si intersecano in un unico punto. Misurando lati e angoli del triangolo otteniamo:
lunghezza della base AB = 3,3, altezza CZ = 1,1
lunghezza della base BC = 3,0, altezza AX = 1,9
lunghezza della base AC = 2,1, altezza BY = 2,5
angolo AXB = angolo AXC = 90°;
angolo BYA = angolo BYC = 90°;
angolo CZA = angolo CZB = 90°;
Se ora proviamo a calcolare l'area del triangolo usando la formula A=bh/2 troviamo che il numero ABxCZ/2 è DIVERSO da BCxAX/2 e da ACxBY/2. Concludiamo allora che in geometria iperbolica la formula A=bh/2 porge tre risposte diverse in relazione al lato che si sceglie come base del triangolo. Ciò risulta chiaramente inaccettabile per cui A=bh/2 non può essere considerata una formula valida per il calcolo dell'area di un triangolo iperbolico.
2 Area del Quadrato
In geometria euclidea un quadrato con il lato di lunghezza unitaria ha area unitaria. In geometria iperbolica, come abbiamo visto in precedenza, non esistono rettangoli e, a maggior ragione, non esistono quadrati. Si può verificare che se un quadrilatero iperbolico ha tre angoli retti allora il quarto angolo è necessariamente acuto (vedi figura 6.2a).
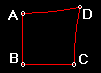
Figure 6.2a: Quadrilatero con 3 angoli retti
Un poligono si dice regolare se ha lati e angoli uguali. Il quadrato rappresenta un esempio particolare di poligono regolare con quattro lati uguali e quattro angoli retti. In geometria euclidea tutti i quadrilateri regolari sono dei quadrati. In geometria iperbolica esistono quadrilateri regolari ma i loro angoli sono acuti. L'area di questi quadrilateri non può essere impiegata come unità di misura per l'area delle rimanenti poligoni come accade per l'area del quadrato di lato unitario in geometria euclidea. Osserviamo ancora che i quadrilateri iperbolici ricoprono il piano in modo particolare. In Figura 6.2b vediamo come nove quadrati 1x1 formino un quadrato 3x3. In Figura 6.2c vediamo come giustapponendo cinque quadrilateri iperbolici 1x1 si ottenga un poligono ben diverso da ciascuno dei poligoni che lo formano.

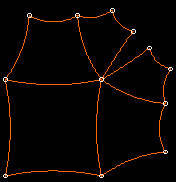
Figure 6.2: Quadrilateri Regolari Congruenti (b) Euclidei (c) Iperbolici.
3 Difetto di un Triangolo
Come abbiamo visto in precedenza, in geometria iperbolica, la somma degli angoli interni di un triangolo è sempre minore di 180°. Chiamiamo difetto di un triangolo l'angolo ottenuto sottraendo a 180° il valore della somma degli angoli interni di un dato triangolo. Costruendo diversi triangoli iperbolici e misurando il loro difetto osserviamo che se il triangolo è "piccolo" anche il suo difetto risulta tale per cui la somma degli angoli interni del triangolo si avvicina al valore 180°. Più precisamente si verifica che al tendere a zero del perimetro del triangolo la somma degli angoli interni tende al valore 180°. Ciò è in armonia con l'idea che parti "piccole" del piano iperbolico hanno una geometria molto simile a quella euclidea. Al contrario per triangoli "grandi" il difetto risulta a sua volta "grande". Al tendere all'infinito delle lunghezze dei lati del triangolo gli angoli tendono a zero e il difetto si avvicina al valore massimo di 180°.
Prima di procedere è una buona idea provare a costruire con NonEuclid alcuni triangoli. Selezionando dal menu "Misure" l'opzione "Misura Triangolo" verranno visualizzate tutte le lunghezze dei suoi lati e le ampiezze dei suoi angoli interni. In questo modo non sarà difficile familiarizzare, fatto importante, con il concetto di difetto di un triangolo.
Il difetto di un triangolo gode di una notevole proprietà: come l'area anche il difetto è additivo. In altri termini se un triangolo, vedi Figura 6.3 in basso, è formato da due triangoli il difetto del triangolo di partenza è uguale alla somma dei difetti dei triangoli che lo formano. Infatti il difetto del triangolo BAM è 77.4°, il difetto del triangolo CAM è 43.7° e il difetto del triangolo ABC è 121.1° e 77.4 + 43.7 = 121.1. Questa proprietà si dimostra sempre valida indipendentemente dal numero di triangoli in cui si divide il triangolo dato. Verificalo usando NonEuclid!
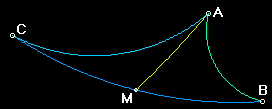
Figure 6.3: Additività del Difetto
4 Difetto di un Poligono
Un qualsiasi poligono può essere diviso in parti triangolari che non si sovrappongono. In Figura 6.4 vediamo due modi di dividere uno stesso poligono in parti triangolari.

Figure 6.4: Decomposizioni di un Poligono
Definiamo difetto di un poligono la somma dei difetti dei triangoli che lo formano. Un poligono può essere diviso in parti triangolari in infiniti modi; tuttavia, la somma dei difetti dei triangoli che lo formano, assume sempre lo stesso valore risultando indipendente dal particolare modo in cui è stata effettuata la suddivisione del poligono. Verificalo usando NonEuclid!
5 Invarianza per Riflessione del Difetto
Abbiamo visto in precedenza che la forma degli oggetti geometrici cambia se su di essi si eseguono riflessioni attorno a rette iperboliche. In qualsiasi modo venga definita l'area degli oggetti geometrici si richiede che il suo valore non cambi passando da un oggetto all'oggetto ottenuto da esso tramite una o più riflessioni. Si richiama all'attenzione il fatto che, nella riflessione di oggetti geometrici iperbolici, le ampiezze dei loro angoli rimangono immutate. Per questo motivo anche il difetto rimane invariante per trasformazioni di riflessione.
6 Proprietà dell'Area
Quando si definisce una procedura per il calcolo dell'area si richiede che [Moise-74]:
Si dimostra che, affinché valgono tutte le proprietà menzionate, è sufficiente scegliere di misurare l'area con la formula A=kd dove d è il difetto e k una opportuna costante. [Moise-74]
La scelta di k è importante in quanto attraverso k si collega la misura del difetto alla misura dell'area.
7 Limite Superiore dell'Area
Una interessante conseguenza della formula A=kd è che l'area massima ammissibile per un triangolo è sempre finita e minore di k180°. E l'area di un poligono è sempre finita? Possiamo intuire che l'area di un poligono assume sempre un valore finito con il seguente ragionamento: immaginiamo di poter costruire un poligono con difetto di 200°. Se ora costruiamo un triangolo che contiene il poligono, dal momento che il difetto del triangolo è pari alla somma delle parti che lo compongono, si arriva all'assurdo per cui il difetto di un triangolo è maggiore di 200°. Allora è impossibile che un poligono abbia un difetto di 200° e ciò dimostra che anche l'area di un poligono assume sempre un valore finito. Vedi gli esercizi sui Poligoni per maggiori dettagli.
 Pagina Iniziale
Pagina Iniziale
 Successivo - Sistemi di coordinate X-Y
Successivo - Sistemi di coordinate X-Y
Copyright©: Joel Castellanos, 1994-2002